Probing Vacuum Entanglement

We demonstrated that Bell's inequalities are violated for arbitrarily far-apart regions in the vacuum. We also showed that as a function of the separation length $L$ between the regions, entanglement decays at slower rate than $Exp( -L^2)$. To this end we employ an approach wherein vacuum entanglement is directly probed in a controlled manner, by letting a pair of initially non-entangled atom-like systems , locally interact with a field for a finite duration, such that the two systems remain in causally disconnected regions throughout the whole process quant-ph/0008006. quant-ph/0212044. By examining the final state of the two systems, we obtain a lower bound on the amount of vacuum entanglement and a condition for a violation of Bell's inequalities in the vacuum quant-ph/0310058..

See also my lecture on  Vacuum-Entanglement delivered at the Conference in honor of Asher Peres's birthday (2004).

Many-Body, ModeWise Entanglement

We found that bi-partite entanglement of bosonic, as well as fermionic, multi-mode gaussian states, has a universal modewise structure that is (up to local transformations) equivalent to products of 1*1 squeezed states for bosonic modes, and to a products of "EPR-like"  states for fermion modes PRA, quant-ph/0404176.  Therefore, with respect to any bipartite division of the modes, pure gaussian states (as well as a class of isotropic mixed states) always display a pairing structure. For fermions this pairing has the form of a BCS-like wave function. This type of structure characterizes the ground states of a large class of quadratic Hamiltonians arising from several interacting models (Hubbard Models, spin-chains, BCS theory) in the mean-field approximation. For bosonic modes this modewise structure characterizes the ground state of Harmonic-chain models.

Entanglement structure of the harmonic-chain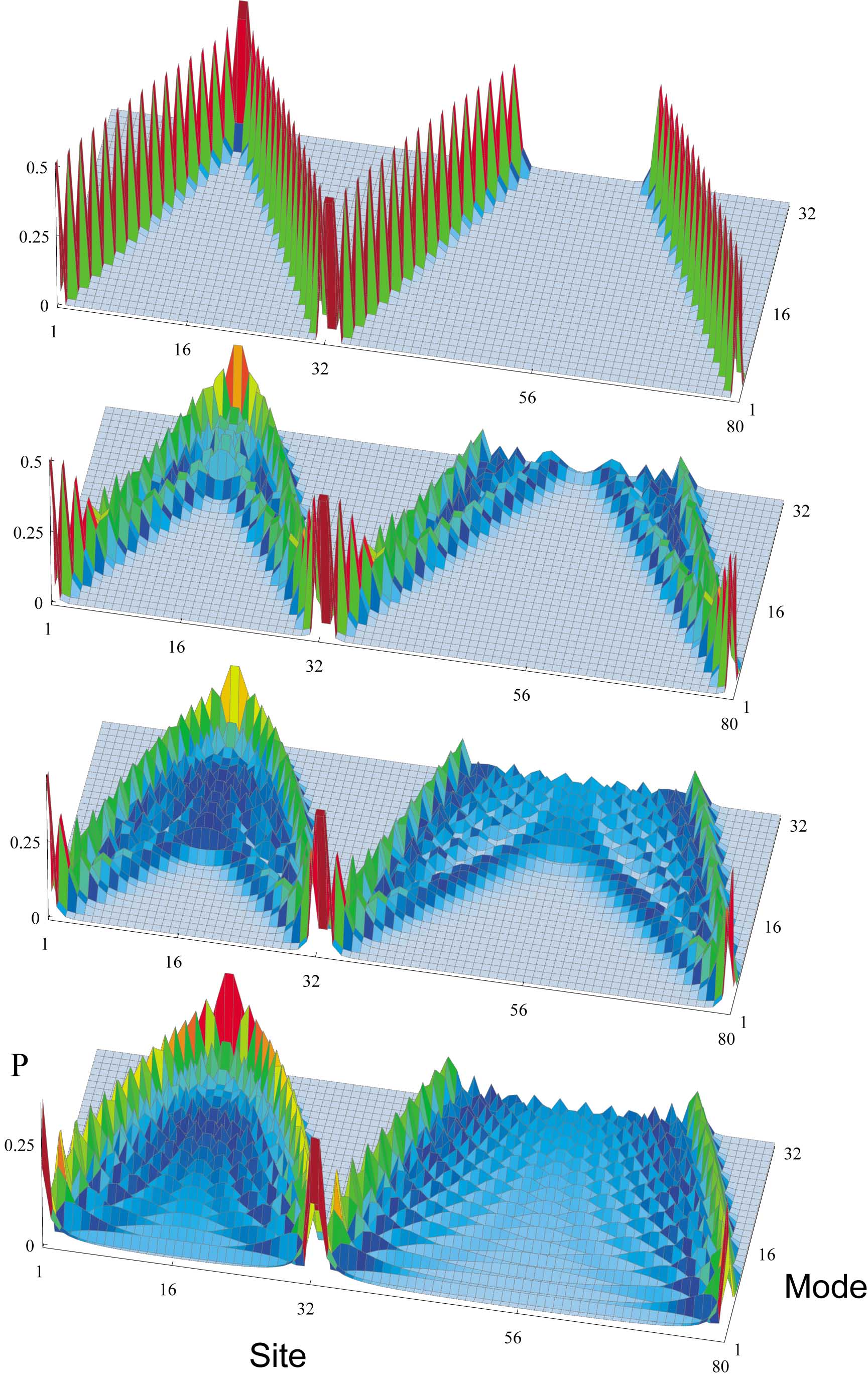

We studied the structure of vacuum entanglement for two complimentary segments of a linear harmonic chain by applying the
modewise decomposition of entangled gaussian states discussed in PRA. We find that the resulting entangled mode shape
hierarchy shows a distinctive layered structure with well defined relations between the depth of the modes, their characteristic wavelength, and their entanglement contribution. We re-derive in the strong coupling (diverging correlation length) regime, the logarithmic dependence of entanglement on the segment size predicted by conformal field theory for the boson universality class, and discuss its relation with the mode structure. We conjecture that the persistence of vacuum entanglement between arbitrarily separated finite size regions is connected with the localization of the highest frequency innermost modes.

For the article see:

A. Botero, and B. Reznik, Spatial Structure and Localization of Vacuum Entanglement in the Linear Harmonic Chain,  Submitted to Phys. Rev. A. (2004). quant-ph/0403233.