Quantum Information Processing with Solitons@Quantum

Solitons are solutions of nonlinear models which are characterized by being localized, nonperturbative and topologically protected. "Localized" means that in an arbitrarily long system with interactions, the soliton remains a nondispersive solution whose energy is usually localized with an exponentially decreasing spatial profile (this is in contrast to linearized phonons). Solitons can often be put into motion in their medium without losing their shape. "Nonperturbative" means that these solutions depend essentially on the nonlinearity of the system, and are singular in the limit of vanishing nonlinearity. "Topologically protected" means that the existence of a soliton solution usually depends on the boundary conditions, and it cannot be "destroyed" by any continous transformation (in particular, time evolution). Solitons are found in many physical systems and are often observed in systems obeying classical physics. In chains of coupled particles, solitons are discrete spatial configurations, as in the Frenkel-Kontorova (FK) model.

The figure schematically shows a soliton in the FK model. The model describes a competition between two energy scales - the nonlinear periodic substrate potential in which the point particles move, and their harmonic spring interaction. If there is exactly one particle less then minima of the potential in an arbitrarily long chain, a single kink soliton is the absolute minimum (ground-state) configuration.

Discrete spatial solitons like that of the FK model and other generalizations are commonly referred to as kinks. The small oscillations of the particles about their location in a static kink configuration can be described in terms of linearized normal modes. An important property of kinks is the existence of localized modes shared chiefly by the particles at the kink core. One mode is the kink's translational "zero-mode", whose frequency generally rises above zero due to the discreteness. Other localized modes are known as "internal modes". Physically they describe "shape-change" excitations of the kink and typically they are separated by an energy gap from other long-wavelength phononic modes. The internal modes, like any linearized harmonic modes, can be canonically quantized in harmonic oscillator operators, and then they describe quantum internal modes of oscillation of the particles, about the classical kink configuration.

Since so many physical systems are eventually nonlinear, the role of solitons in the context of Quantum Information Processing (QIP) is an extensive subject. In this project we focus on the possible usage of solitonic internal modes as carriers of quantum information, and their use for studying Quantum Information Theory concepts. We have investigated the coherent quantum time-evolution of kink internal modes in different discrete models like the Frenkel-Kontorova (sine-Gordon) and the double-well φ⁴. The strong nonlinearity responsible for the formation of the localized modes of a soliton, is responsible for introducing nonlinear coupling between the localized modes and all other modes. We have found long coherence times for the internal modes, taking into account the full affect of nonlinearity and discreteness at realistic finite temperatures.

The ability to control quantum coherence in ion traps has increased dramatically in recent years. Quantum simulation schemes were proposed for the ion trap and realized. High fidelity gates have been performed and multi-partite entangled states created. We have shown that solitons may be realized in existing ion traps, and that coherence persists in the internal modes for long times at a Doppler-cooled trap. This could allow the direct manipulation and measurement of internal quantum dynamics of discrete static solitons in a linear ion trap.

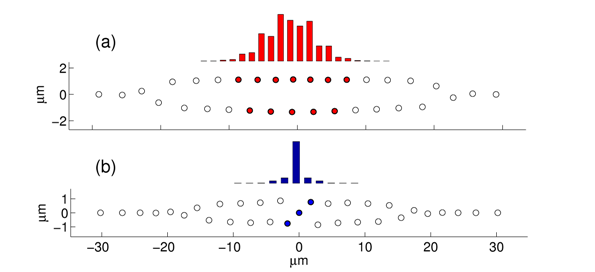
"Kink" solitons are metastable excitations of the zigzag phase of an ion chain, stable at up to ~15 times the Doppler temperature according to numerical simulations.(a) An extended kink, obtained at weak transverse trapping. A localized internal oscillation (red bars) involves ~10 ions. (b) A highly discrete kink, at strong transverse trapping. The localized internal mode (blue bars) involves mostly the 3 core ions. Reproduced from [2].

By use of the advanced QIP technology and control of trapped ions, a soliton may be put into superposition in the laboratory. The rich nonlinear dynamics of solitonic internal modes can be manipulated and measured with unprecedented accuracy.

Ion trap kinks are currently being studied experimentally in a several groups around the world. The Freiburg group has recently observed different types of kinks, and novel dynamical features of these kinks have been explored. The kinks show a high amplitude motional excitation even while being continuously laser-cooled, which turns out to be a strongly anharmonic oscillation of the kink's lowest-frequency, localized mode. In addition to this nonlinear motion, we find parameter regimes such that the local periodic Peierls-Nabarro potential experienced by a discrete kink becomes a globally confining potential, capable of trapping one cooled defect at the center of the crystal.

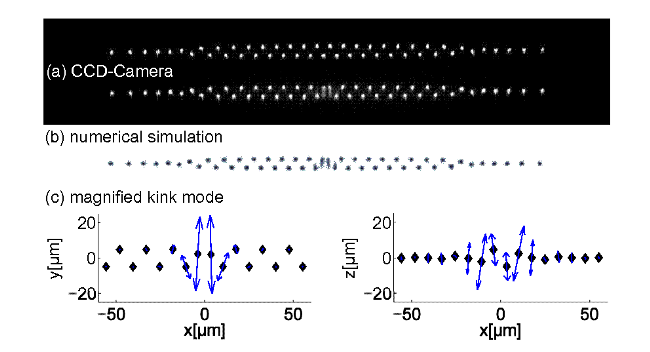
Coulomb crystals with 50 ions. (a) CCD images of two crystals obtained for identical experimental parameters. Top: a pure zigzag featuring the minimal energy configuration. Bottom: two central ions clearly deviate and show a blurred extension in the radial direction. (b) Integrated numerical results for the structure depicted in (a)-Bottom, projected onto the crystal plane. The agreement of theory and experiment is very high. (c) Numersically derived components of ion oscillations in the localized, low-frequency normal mode of the kink, in (perpendicular to) the crystal plane, are depicted on the left (right). Reproduced from [1].

1. Entanglement Generation Using Discrete Solitons in Wigner Crystals
   H. Landa, A. Retzker, T. Schaetz and B. Reznik
   Submitted to Phys. Rev. Lett. ; arXiv:1308.2943
2. Structure, dynamics and bifurcations of discrete solitons in trapped ion crystals
   H. Landa and B. Reznik
   J. Brox, M. Mielenz and T. Schaetz
   New J. Phys. 15, 093003 (2013) ; arXiv:1305.6754
3. Trapping of Topological-Structural Defects in Coulomb Crystals
   M. Mielenz, J. Brox, S. Kahra, G. Leschhorn, M. Albert and T. Schaetz
   H. Landa and B. Reznik
   Phys. Rev. Lett. 110, 133004 (2013) ; arXiv:1211.6867
4. Quantum Coherence of Discrete Kink Solitons in Ion Traps
   H. Landa, S. Marcovitch, A. Retzker, M. B. Plenio, and B. Reznik
   Phys. Rev. Lett. 104, 043004 (2010) ; arXiv:0910.0113
5. Coherence properties of discrete static kinks (Master Thesis)
   H. Landa
   arXiv:0910.0109
   
6. Entanglement of Solitons in the Frenkel-Kontorova Model
   S. Marcovitch and B. Reznik
   Phys. Rev. A 78, 052303 (2008) ; arXiv:0809.1857
   

For more references on this subject please see the links above.

• The quantum optics group at the University of Ulm, headed by Prof. Martin Plenio.
• Dr. Alex Retzker at the Hebrew University of Jerusalem.
• The experimental atomic-, molecular- and optical physics group at the University of Freiburg, headed by Prof. Tobias Schaetz.