Introduction to Planetary Science

Recommended reading: Worlds Apart by G. J. Consolmagno and M. W. Schaefer. Prentice Hall, New Jersey, 1994.

1. Introduction to the introduction

1.1. What do we see in the sky?

1.1.1. Clouds.

1.1.2. Meteors.

1.1.3. Comets.

1.1.4. Birds.

1.1.5. Sun.

1.1.6. Moon

1.1.7. Aurora

1.1.8. Stars

1.1.9. Planets – Planets are different from stars as will be explained below.

1.2. What are planets from the observational standpoint?

1.2.1. There are fixed stars in the sky.

1.2.2. They are arranged in constellations.

1.2.3. They rise and set like the sun. Every night the same stars rise a little earlier. This was originally explained by saying that the stars sat on a celestial sphere that rotated about the Earth.

1.2.4. There are some “stars” that behave differently from the others. Whereas the ordinary stars are arranged in constellations and their relative positions are fixed, there are “stars” that wander through the sky. The Greek name for these wanderers is “planets”.

1.2.5. The planets are limited to a strip of the celestial sphere called the zodiac. .

1.2.6. Planets have a complex motion with respect to the background stars, which includes retrograde motion. The ancient astronomers tried using epicycles to explain this motion, but the number of epicycles needed for a good fit to observations grew too large to be believable. Now we explain it with a heliocentric theory that has the Earth and all the planets going around the Sun. This theory is not only conceptually simpler, but also gives a much better fit to observations.

1.2.7. The heliocentric theory also explains the changes in the seasons.

1.2.7.1. Seasonal changes involve not only changes in weather, but also changes in the stars overhead.

1.2.7.2. The Earth's rotation axis is tilted 23.5° from the vertical to the ecliptic and the direction of the axis is fixed in space.

1.2.7.3. When the axis points towards the Sun, the northern hemisphere gets more sunlight and it is summer there. Half a year later the southern hemisphere experiences summer. .

2. What can we learn about this solar system that we live in?

2.1. How big is the solar system, i.e. what are the distances between the planets?

2.2. The Greeks noted that Venus is never more than 47° from the Sun, and Mercury is never more than 28° from the Sun.

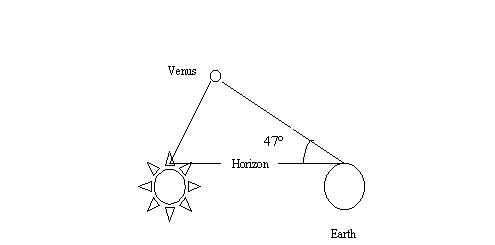
2.3. At maximum elongation the angle Earth-Planet-Sun = 90°.

2.4. Call the distance from the Earth to the Sun 1 AU (astronomical unit) then

2.4.1. The distance of Venus from the Sun is sin 47 = 0.7 AU.

2.4.2. The distance of Mercury from the Sun is sin 28 = 0.4 AU. This assumes the orbits are all in the same plane.

2.5. We still need to know big an AU is.

2.5.1. In 275 B.C.E. Aristarchus of Samos tried to solve the problem. It had been suggested by Heracleides of Heraclea Pontica that Mercury and Venus went around the Sun. Aristarchus assumed that since the Moon went through phases, and we saw only one side, then the Moon must go around the Earth, and the phases are caused by solar illumination. The angle at which we see the first quarter depends on the distance of the Sun. By counting the number of days after new moon that one saw exactly the first quarter, and by knowing that a full 360° revolution took about 27 days, he was able to measure the angle as 87°. This meant the Sun was 1/cos(87°) = 19 times further away than the Moon.

2.5.2. Actually, the correct angle is 89.85° and the true factor is 390.

2.5.3. Since the Sun was so far away, and Mercury and Venus orbited it, Aristarchus suggested that the Earth orbited it as well (1700 years before Copernicus).

2.5.4. We still don't have a distance in km. however. The Greeks never solved the problem, but did solve others.

3. How big is the Earth?

3.1. About 225 B.C.E. Erastothenes of Cyrene ran the library in Alexandria. They called him Beta (Aristotle was Alpha). He was told that on a certain day of the year at noon the sun did not cast any shadows in Syene. On that same date the shadows in Alexandria, 5000 stadia (about 800 km) to the north were 1/8 the size of the object casting them. This meant that the Sun made an angle of tan^-1(1/8) = 7.13º with the zenith.

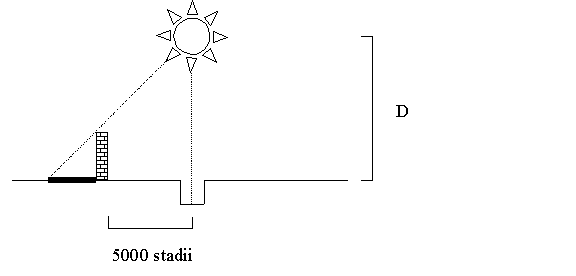
3.2. If you assume that the Earth is flat this puts the sun at a height of 6400 km. . This is much too close. What is wrong?

3.3. The angle is not caused by a nearby Sun, but by the fact that the Earth is round. The Greeks surmised that this is the case because

3.3.1. The Moon is round.

3.3.2. The Sun is round.

3.3.3. They could see the Earth's shadow on the moon during a lunar eclipse.

3.3.4. The tides are similar in the Atlantic and Indian oceans, and Erastothenes thought you could sail around Africa to reach India.

3.3.5. He even suggested you could sail westward from Spain to reach India (1700 years before Columbus).

3.4. So you assume the Sun is much further away than an Earth radius so that its rays are parallel. You also need to assume that Alexandria is due north of Syene.

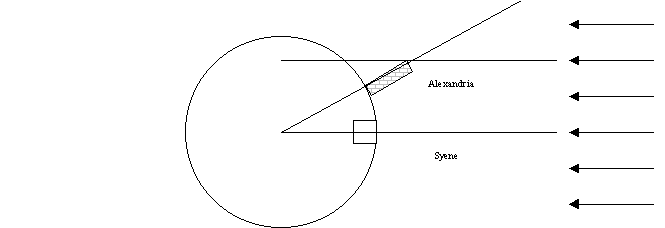
3.5. Geometry then gives you that the radius of the Earth is 8x5000 = 40,000 stadia or about 6400 km. The circumference is then 40,200 km, which is close to the correct value of 40,030 km.

3.6. If we assume that the other planets are similar to the Earth, they too should be thousands of km in diameter.

4. Hipparchus tried to measure the A.U. in 150 B.C.E

4.1. When the Moon eclipses the Sun, the two bodies appear to be nearly the same size.

4.2. When the Moon eclipses the Sun, the Moon's shadow is very small, essentially a point.

4.3. By similar triangles, since the Sun is 19 times further than the Moon (Aristarchus, 275 B.C.E.), the Sun must be 19 times larger than the Moon, but how large is the Moon?

4.4. When the Earth throws its shadow on the Moon, that shadow is much larger than the Moon (2.5 times). Since we know the diameter of the Earth, we can set up a system of equations based on similar triangles: Let EM be the Earth-Moon distance, M be the diameter of the Moon, D the diameter of the Earth, and x the distance from the apex of the Earth's shadow to the Earth. We then have, from the big triangle

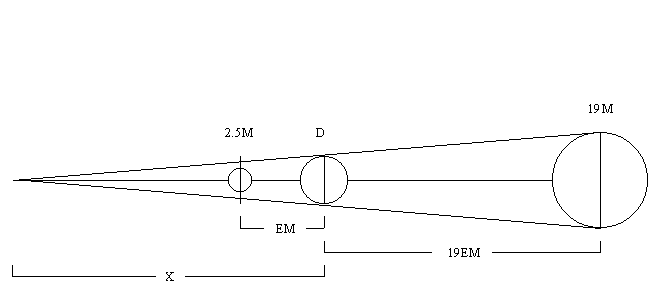
4.5. The little triangle gives

4.6. The first equation gives

4.7. while the second gives

4.8. Equating these two relations gives M = 0.30D. We now have a value for the diameter of the Moon: 3800 km. The actual value is 3450 km. We have learned that the Moon is a planetary-sized body.

4.9. From Aristarchus we know that the Sun is 19 times larger than the Moon, and has a diameter of 73,000 km. In fact the solar diameter is about 20 times larger, but that is due to the error Aristarchus made in measuring the angle.

4.10. The distances can be found by measuring the angle distended by the Moon. The result gives a distance EM = 450,000 km (the real value is about 400,000 km), and the distance to the Sun as 7,600,000 km (again about a factor of 20 wrong). In any case, we have some notion of the size and distance of solar system objects.

5. A much more accurate way of measuring the distance to the Sun is to use transits of Mercury and Venus.

5.1. The angular size of the Sun is about 0.5°, so the diameter of the Sun is sin 0.5 = 0.01 AU.

5.2. We can measure the diameter of the Sun by observing a transit of Mercury or Venus.

5.3. If you observe the time to transit from two places on Earth, the parallax allows you to compute the Sun's diameter in terms of Venus' distance from the Sun, and hence in terms of the AU. This lets you find the AU directly.

5.4. Because of the tilt of the orbit, transits are rare. Kepler (1629) found that, for Venus, they occured in pairs, 8 years apart, about once a century.

5.4.1. Jeremiah Horrox observed a transit in 1639, and realized how it might be used, but never published details.

5.4.2. James Gregory elaborated on the idea in 1663.

5.4.3. Edmund Halley (1716) gave all the details. The next transits were in 1761 and 1769, and Halley left detailed instructions on how to do the calculations. The story of these observations is fascinating.

5.4.4. The value was improved during the transits of 1874 and 1882, and they give the value of 1AU = 150,000,000 km that is used today.

5.4.5. The next transits will occur on June 8, 2004 and on June 6, 2012. Get ready!

6. Other sizes and distances.

6.1. The angular diameter of Venus is about 1 arc-minute. From this and the AU we get the diameter of Venus to be about 12,000 km, just less than that of the Earth.

6.2. Other planetary distances and diameters can be found from Kepler's laws and similar considerations.

7. The Sun

7.1. What is the Sun? We all know it is a star, but what about it's other properties.

7.2. We can measure the radius of the Sun. R_s = 6.96x10¹⁰ cm = 109 R_e.

7.3. We can measure the mass by using the size of the AU and the fact that the Earth orbits in one year. Equating the centrifugal and gravitational forces

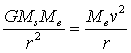
where v is the speed of the Earth in its orbit around the Sun. The can be found from

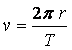
where T is the time it takes the Earth to make one orbit. The result is M_s = 1.99x10³³ g = 333,000 M_earth.

7.4. The Sun is orders of magnitude larger than the Earth.

7.5. We are 1.5x10¹³ cm from the Sun, but we still feel its warmth.

7.6. The energy flux through any sphere concentric with the Sun must be constant if there are no other sources or sinks, so if L is the rate of energy production (erg s^-1) and R is the distance from the sun, then

7.7. The luminosity is also related to the effective temperature by

7.8. From this it follows that if R_s and T_s are the radius and temperature of the Sun, and r_e and T_e the distance from the Earth to the sun and its temperature, then the amount of energy put out by the Sun per second is

7.9. and the amount of energy reaching the Earth per square centimeter times its cross section is

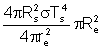
where r_e the radius of the Earth. We can equate this with the energy reradiated by the Earth in steady state (4p s R_e² T_e⁴).If we take T_e = 280 K, we find that T_s = 5800 K. The Sun is hot.

7.10. We can also compute the luminosity. L = 3.9x10³³ erg s^-1. So there is an enormous energy source inside the Sun.

7.11. Can we check any of this?

7.11.1. We can estimate the surface temperature from a black body.

7.11.2. A body in equilibrium with a surrounding electromagnetic field (like in a heated cavity) will give the radiation a form that is related to its temperature. The energy density at a given wavelength, l, is given by

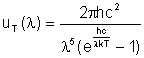
7.11.3. where k is Boltzmann's constant c is the speed of light, and h is Planck's constant. This is known as the Planck function. If we differentiate with respect to wavelength, and substitute for the various constants we get the Wien displacement law l_maxT = 0.3 cm K.

7.11.4. If we plot the amount of energy the Sun emits at different wavelengths, we can get something that looks like a black body curve. It won't be exactly right because

7.11.4.1. The light comes from different layers at different temperatures.

7.11.4.2. Some of the light gets absorbed on its way out.

7.11.5. In reality you need detailed models of the radiative transfer, but what comes out is that the temperature really is around 6000 K near the surface.

7.12. The Sun contains most of the mass (99.9%) of the solar system, and therefore the center of mass of the solar system is close to the center of mass of the Sun.

8. What is the Sun made of?

8.1. The mass and radius give us a density of 1.41 g cm^-3.

8.2. Does that mean that the Sun is composed of water + some heavier material, or is this just an effect of pressure. What is the pressure inside the Sun?

8.3. Imagine a spherical shell inside the Sun with an inner radius of r and a thickness dr. The pressure at the inner surface is P(r) and at the outer surface P - dP. The difference, dP comes from the additional weight of the layer itself. The layer has a volume 4p r² dr. If the density in this region is r(r) then the weight is the density times the volume, and the pressure is the weight divided by the area. Thus

8.4. This is the equation of hydrostatic equilibrium. In deriving it we have assumed that the material making up the body has no internal forces (i.e. it acts like a liquid ... the hydro in hydrostatic). We have also assumed that the configuration is not accelerating (... static). Finally, for simplicity in deriving the equations I have assumed that the body is a sphere, and that the density distribution is spherically symmetric, but these assumptions are not essential to the argument.

8.5. There are still more unknowns than equations, but we can easily find a relation between M(r) and r(r) by demanding mass conservation:

8.6. We still need some relation between the pressure and the density (equation of state), but this depends on the composition, and the temperature. Thus we need to introduce another variable, T(r). The variation of T will depend on details of energy transfer, so we need to include information about opacity, conductivity and convection. We will look at some of these issues later. For the moment we ignore these details.

8.7. The pressure equation gives

8.8. We can define an average density, <r(r)> as the average density of the material contained in the volume within a distance r from the center:

so that

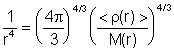
which can be substituted to give

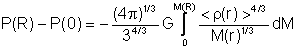
8.9. We make two assumptions

8.9.1. P(R)<<P(0)

8.9.2. r(r) does not increase as r increases. This means that <r(r)> ³ <r(R)>

8.10. This gives

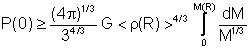
8.11. On integration we get

which gives an lower limit to the central pressure. For the case of the Sun, this corresponds to a pressure of P(0) ³ 10³ Mbar. In fact, since the central densities are much much higher than the average density, the central pressure is expected to be much higher than this as well. For the Earth, where the density changes are much less, this approximation gives a central pressure of about 1.5 Mbar, while detailed models give a pressure of 3.5 Mbar. In any case, the pressure in the Sun is enormous.

8.12. The temperature inside the Sun can be estimated.

8.13. The gravitational binding energy of the Sun is roughly

8.14. The thermal energy (assuming the Sun has some characteristic temperature) is

where N₀ is Avogadro's number, k is Boltzmann's constant, and m is the mean molecular weight. Taking m = 1 as representative, and equating the thermal and gravitational energies, we get T ~ 10⁷ K which is the right order of magnitude.

8.15. Assuming an ideal gas, we have

which gives a density of the order of 1 g cm^-3. This is consistent with the assumption that the density is everywhere roughly equal to the average density. Since it is not, and the pressure at the center is really much higher, the actual density there will be much higher.

8.16. We can now begin to understand how the Sun gets its energy ... from nuclear reactions.

9. The Sun like all other stars has a nuclear reactor in its center, and that supplies the energy. This is the difference between stars and planets.

9.1. The large mass of the star produces huge pressures and temperatures near the center.

9.2. If the configuration is to remain stable against collapse, it must be very hot. The thermal energy is supplied by nuclear reactions.

9.3. A neutron, left to itself is unstable and breaks up into a proton, electron, and anti-neutrino. The reverse reaction p ® n + e⁺ + n does not occur naturally since it violates conservation of energy. In the presence of a second particle, some energy can be “borrowed” from the surrounding field, and the reaction can proceed. This requires high density and temperatures of about 10⁷ K. It is also rare.

9.4. If it does happen and the resultant neutron combines with a proton, then resulting reaction is p + p ® D + e⁺ +n. The cross section is 10^-47 cm² under the appropriate conditions and it produces 1.28 MeV of energy.

9.5. The resultant D will immediately combine with a nearby proton to give D + p ® ³He + g. I will write this as D(p,g)³He. The reaction releases 5.49 MeV.

9.6. The ³He could wait around until another proton turned into a neutron in its presence, and then capture it to become ⁴He, but that is extremely rare. Instead, ³He builds up until one helium can give up its neutron to another to make ⁴He. The reaction is written as ³He + ³He ® ⁴He + 2p and releases 12.9 MeV of energy. No nuclei of atomic number 5 exist, so the sequence terminates here. This is the sequence of reactions that keeps the Sun burning.

9.7. About 10% of the Sun is under the right conditions for this to happen.

10. How does this energy get out of the Sun?

10.1. The resultant energy is produced as gamma ray photons. These are not absorbed in the Sun since there is nothing to absorb them, but they do get scattered. They have a random walk with a mean free path that is very short and it takes millions of years for them to reach the outer layers of the Sun. Even so radiation is the most efficient method of transferring energy. For the Sun the mean free path of a photon is roughly a cm. The radius of the Sun is about 7 x 10¹⁰ cm, and a random walk with n steps of size x will carry you approximately a distance of xÖn, so to travel through most of the Sun, the photon will have to take 10²² steps, and so travel a total distance of »10²² cm. Even at the speed of light, this takes some 10⁴ years.

10.2. In the outer layers the temperature is low enough so that electrons and nuclei can recombine. At this point a gamma ray can tear them apart again and be absorbed in the process. Since the heat cannot be transferred efficiently by radiation the temperature gradient builds up until convection begins.

10.2.1. Convection is a much more efficient process process for transferring energy than radiation. The density difference between hot matter and colder matter is

and the upward buoyant force per unit volume is

which gives an acceleration of

10.3. The time to travel the radius of the Sun, taking DT/T = 1, M = 2 x 10³³ g, and r = 7 x 10¹⁰ cm, is

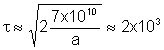sec.

10.4. This is much much faster.

10.4.1. The problem is that it only happens under special conditions. Consider a blob of matter rising to a region of lower temperature. Since the pressure is lower there, it also expands and cools adiabatically. It will rise from a region where the pressure is P, the temperature, T, and the density r, to a region where the pressure is P', etc. The blob will continue to rise so long as it is less dense than its surroundings, i.e. r_blob < r'. Since the pressure inside the blob is equal to that outside, this means that in order for convection to be active we need T' < T_blob. But T' = T - dT, while T_blob = T - dT_adiab, so the condition for convection is

so that convection will only start up in a region where the temperature gradient is high enough, i.e. where the opacity is high enough.

10.5. The Sun is thus built up of a radiating core, a convecting layer near the surface, and then an outer radiating region called the photosphere. . Some of the convection reaches the surface, and we see granulation.

10.6. Above the photosphere is the chromosphere, a thin atmosphere of gas extending about 2000 km. .

10.7. Above that is the corona. . This region can actually reach temperatures of 10⁶ K, which would seem to violate the first law of thermodynamics. In fact it is heated from below by mechanical means, and has an unstable outer layer where the solar wind is formed

11. Sunspots

11.1. Sunspots can be seen easily on the Sun.

11.2. The background temperature in the Sun is about 5770 K, while in a sunspot it is about 4500 K. As a result they must be denser than their surroundings, and so must somehow be supported against gravity.

11.3. They are found between 5° and 40° from the equator, and are seen in pairs.

11.4. They move slowly across the surface of the Sun, and the number changes with time. There is an 11-year cycle, which culminates in a time when there is a minimum of sunspots. This is called the quiet Sun period

11.5. The explanation of this phenomenon is that the sunspots are regions where the Sun's magnetic field is breaking through the surface. The background field is typically 2 x 10^-4 telsa, but in sunspots it can be 0.0025 to 0.05 telsa. Sunspots appear in pairs, one being where the field emerges at the surface, the other where it re-enters the Sun. At the end of the 11-year cycle the field changes polarity, so that a complete cycle is 22 years (see picture of sunspot pair).

11.6. Magnetic activity in the Sun is also responsible for solar flares and for the solar wind. (see picture of solar flare)

12. Solar neutrinos

12.1. It would be very nice to be able to check our theories by looking into the center of the Sun. This is possible through neutrino astronomy. Neutrinos have a very small cross-section for interaction with matter, so you fill a gold mine (to keep out extraneous radiation) with 400,000 liters of C₂Cl₄, and look for the reaction

³⁷Cl + n ® ³⁷Ar + e^-

which should produce a few atoms of radioactive argon per month. You flush out the detector ever few months and count the number of atoms. At present the experimental value is 2.1 ± 0.3 SNU (Solar Neutrino Units) while the best theoretical models give 5.8 ± 2.2 SNU. The agreement is not very good and people have been looking for possible explanations.

12.2. One problem is that this experiment sees only high-energy neutrinos. The sequence

p + p ® D + e^- + n

D + p ® ³He + g

³He + ³He ® ⁴He + 2p

produces neutrinos with a maximum energy of 0.42 MeV. These are not energetic enough to be detected by the chlorine experiment. Instead we see the neutrinos from a less common reaction sequence

³He + ⁴He ® ⁷Be

⁷Be + p ® ⁸B + g

⁸B ® ⁸Be* + e⁺ + n

⁸Be* ® 2⁴He

12.3. This reaction produces 14 MeV neutrinos and these are seen. It would be nice to check the first reaction, which is far more important. These less energetic neutrinos can be detected via the reaction

⁷¹Ga + n ® ⁷¹Ge + e^-

but for this you need about 30 tons of Ga, which is a rare earth. Currently the GALLEX detector is being run using GaCl₃. We should know more in the next few years.

12.4. A second possibility comes from high-energy physics theories that suggest that the neutrino has a finite rest mass. In this case some neutrinos might switch to another type on their way to Earth, and thus escape detection.

12.5. The internal structure of the Sun can also be probed by heliseismology. Here you study the vibrations of the Sun in an attempt to determine the density distribution inside it. This is a relatively new field, but the results tend to confirm the picture developed from other means.

13. Nucleosynthesis

13.1. Where do the elements that make up our solar system come from, and what are their abundances?

13.2. H and He were formed mostly in the big bang, although some He is formed in stars.

13.3. We have seen how hydrogen burns to form helium, but this is a slow reaction. There is an alternative that is important is some stars

p + ¹²C ® ¹³N + g

¹³N ® ¹³C + e⁺ + n

¹³C + p ® ¹⁴N + g

¹⁴N + p ® ¹⁵O + g

¹⁵O ® ¹⁵N + e⁺ + n

¹⁵N + p ® ⁴He + ¹²C

or

¹⁵N + p ® ¹⁶O + g

¹⁶O +p ® ¹⁷F + g

¹⁷F ® ¹⁷O + e⁺ + n

¹⁷O + p ® ⁴He + ¹⁴N

13.4. This is known as the CNO bi-cycle, and can only work in stars that have a background supply of ¹²C to begin with, i.e. stars that are made of material from an earlier generation of nucleosynthesis.

13.5. When the supply of hydrogen in the core of the star is exhausted it collapses under the pressure, and will continue to collapse unless another fuel is found. ⁴He + ⁴He ® ⁸Be won't work because it is unstable and decays back to He in 10^-16 s. But it can hold the two heliums together long enough for a third He to join and form ¹²C. This happens under conditions of T = 10⁸ K and very high density, i.e. after the core has contracted. In such a case the outer envelope of the star expands and we get a red giant.

13.6. When this fuel is exhausted, C burning begins and helium is added to form ¹⁶O or two ¹²C's are combined to give ²⁴Mg. ²⁰Ne can be formed in this way and so can all the elements up to ⁵⁶Fe, but only if their atomic number is a multiple of 4. As long as the star is massive enough it will continue to contract until the next burning stage is reached. If it is not massive enough, the contraction is halted when the material cannot be squeezed any further. The result is a white dwarf, followed by a red then black dwarf.

13.7. If the star is massive enough it can get all the way to ⁵⁶Fe. At this stage something else happens. ⁵⁶Fe is the most tightly bound nucleus. Further fusion requires addition of energy. Fission does too, so the ensuing collapse is not halted and becomes catastrophic. The result is a type II supernova. This is an excellent means of mixing the elements made till now in with the rest of the interstellar medium.

13.8. What about the rest of the elements that are not multiples of 4?

13.9. There are still protons around, so we can get

p + ²⁰Ne ® ²¹Na

but this is unstable and decays into

²¹Na ® ²¹Ne + e⁺ + n

so we have produced a nucleus with atomic number 21. But this can react with a He to give

²¹Ne + ⁴He ® ²⁴Mg + n

13.10. The magnesium we could have gotten from previous reactions, but here the interesting thing is the neutron. It can combine with some other nucleus (like ⁶⁶Zn) to form a heavier isotope, and to follow a path known as the S-process (slow process).

13.11. If there are reactions that produce many neutrons, the reaction path will follow that of the R-process (rapid process). Other processes occur as well. These happen in various stages of stellar evolution such as novae and supernovae. The point is that current elemental abundances depend on the history of nucleosynthesis in the galaxy.

14. So how is a star different from a planet?

14.1. Perhaps the first question to ask is how planets differ from ordinary rocks. The thing that keeps me from going through the floor is the repulsion between atoms and molecules. These sit in lattice sites in the solid, and what makes the material solid is the forces that keep the molecules in those sites. We can think of these as springs holding the particles in place. If I increase the gravitational force (i.e. the pressure on the material) I can affect those springs. Typically, the pressures involved are about 10⁶ - 10⁸ dynes cm^-2. We can make a simple estimate of how large a body has to be to get these pressures. The pressure is the force divided by the area. The area is approximately 4p R², and the force is the force of gravity, Mg.

14.2. For a planet with a density of about 1 g cm^-3 (which is typical for an icy body), this gives R » 100 km. Icy bodies larger than this would be expected to be round. Rock is stronger than ice, but its density is higher as well, so the numbers stay about the same.

14.3. As the pressure increases, the material flows, but the atoms and molecules still maintain their identities. Eventually the molecules break down, and shortly thereafter the atoms do too. At this stage we may say we have gone from planet to star.

14.4. In a simple (e.g. Bohr) model of an atomb the nucleus has a radius of about 10^-13 cm, and the electron cloud has a radius of about 10^-8 cm. For a hydrogen atom, the energy of the electron in the field of the proton is

where p is the momentum, e the electric charge, m the mass of the electron, and r the distance from the nucleus. The quantum mechanical wavelength of the electron is l =h/p where h is Planck's constant. If R is the radius of the electron's orbit, and l = 2p R, then we get

for stability we want this energy to be a minimum, i.e. dE/dR = 0. This gives

14.5. a₀ is called the Bohr radius, and is a natural unit of atomic distance. The corresponding energy is

14.6. This unit of energy is called a Rydberg and is the natural unit of atomic energy. For the case of an atom with Z electrons, a_z = a₀/Z and E_z » ZE₀. The equality is not exact because of shielding from the inner electrons.

14.7. The pressure associated with the electron cloud can be estimated from

14.8. E is composed of a kinetic and a potential term, so P can be written as P = P_k + P_v where (for a hydrogen atom)

which represents the repulsion due to the kinetic energy of the electron which keeps it from falling into the nucleus, and

which is the coulomb attraction.

14.9. At R = a₀ the pressures are equal and the atom is in equilibrium. At this point the pressure is about 300 Mbar. This is roughly the pressure at which atoms begin to break down, and may be considered to define the place where the body stops being a planet. This occurs at a radius of around 10¹⁰ cm. The radius of Jupiter is around 7 x 10⁹ cm, so it is near the upper limit of what we would consider a planet.

14.10. A star also burns, and more detailed calculations show that this begins at masses of about 70 Jupiter masses. The range in between is filled with brown dwarfs. These are objects that are hot because of their accretional energy, but are not massive enough to be stars. Because they are hot, they glow for a while (some 10⁹ - 10¹⁰ years depending on mass), hence the name.

They can be identified by their mass if they are in orbit, and by the presence of Li in the atmosphere if they are isolated (Li is quickly burned in any nuclear reactions). Some failed stars (those that burn deuterium only) will also burn Li, so there is some ambiguity. But a number of brown dwarfs have been found and it has become a new field of study.