


Next: remarks:
Up: Q-learning and SARSA algorithms
Previous: Q-learning and SARSA algorithms
Q-learning
Lets consider Value Iteration Algorithm(VI) from lecture 6.It described the non linear
operator: L. In every iteration of the algorithm we operate L:
Vn+1=LVn, and explicitaly:
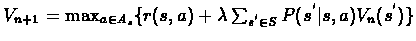 .
.
Lets refine the equation a somewhat. We define new function Q regarding VI:
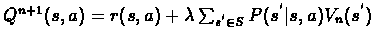 .
.
Now the iteration of VI are:
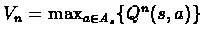 .
Expressed in Q function terms only we have:
.
Expressed in Q function terms only we have:
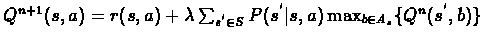 .
.
We write the iteration with
 .
.
(In lecture 7 we learned it converges the right value.)
![$Q^{n+1}(s,a) = (1-\alpha)Q^{n}(s,a) + \alpha[ r(s,a) + \lambda\sum_{s^{'}\in %
S}P(s^{'}\vert s,a)\max_{b \in A_{s}}\{Q^{n}(s^{'},b)\}]$](img35.gif)
Until now the iterations are equvivalent to VI. Instead of taking the excpetancy of the
value of the next step we take a sample of the next step. We assume that we are in state s,
we take action a, the next state s' is distributed by
P(s'|s,a). Finally we get
![$Q^{n+1}(s,a) = (1-\alpha)Q^{n}(s,a) + \alpha[ r(s,a) + \lambda\max_{b \in %
A_{s^{'}}}Q^{n}(s^{'},b)\}]$](img36.gif)
Figure 9.1:
Algorithm for Q-LEARNING
![\framebox[\textwidth]{
\begin{minipage}{\textwidth}
\begin{tabbing}
\ \ \ \ ...
...for}\ \-\\
{\small\bf end} \sc q-learning\-\\
\end{tabbing}
\end{minipage}}](img37.gif) .
. |
Yishay Mansour
2000-01-07