


Next: About this document ...
Up: No Title
Previous: SARSA
Convergence proof
The general idea is writing our algorithm as:
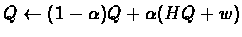
where:
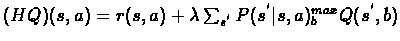
We will show that H is a contracting mapping (operator):
![$\vert\vert HQ_{1} - HQ_{2}\vert\vert = \vert\vert\lambda P[MQ_{1} - MQ_{2}]\vert\vert$](img44.gif)
where
(MQ1)(s)=maxaQ1(s,a). Note that
MQ1=V1. We have,
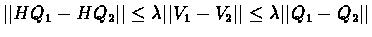 ,
,
Therefore H is 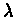 contracting.
contracting.
The parameter w is "noise" in the sample whose expectation is 0.
By using the contracting property of H we show convergence.
For convergence we require:
-
![$Q^{n+1}(s,a)=(1-\alpha_{n}(s,a))Q^{n}(s,a) + %
\alpha_{n}(s,a)[r(s,a)+\lambda^{max}_{b}Q^{n}(s^{'},b)]$](img47.gif)
- Let Ts,a be the time we are in state s and make action a
- Ft is history untill time t
- Thus the algorithm can be written as:
![$Q^{n+1}(s,a)=(1-\alpha_{n}(s,a))Q^{n}(s,a) + \alpha_{n}(s,a)[(HQ^{(n)}(s,a) + %
w_{n}(s,a)]$](img53.gif)
where:
![$w_{n}(s,a)=\lambda[^{max}_{b}Q^{(n)}(s^{'},b)-%
\sum_{s^{''}}P(s^{''}\vert s,a)^{max}_{c}Q^{(n)}(s^{''},c)]$](img54.gif)
- because s' is distributed according to P(.|s,a) (the policy is stationary) then
we have:
![$E[w_{n}(s,a)]=\lambda[E[^{max}_{b}Q^{(n)}(s^{'},b)]-E[^{max}_{c}Q^{(n)}(s^{''},c)]] = 0$](img55.gif)
Therefore the expectation of "noise" is 0.
Theorem 9.1 (A general theorem for Stochastic processes)
Let:
![$r_{t+1}(i)=(1-\alpha_{t}(i))r_{t}(i)+\alpha_{t}(i)[(Hr_{t})(i)+w_{t}(i)]$](img56.gif)
Given that:
- 1.
-
E[wt(i)|Ft]=0
- 2.
-
![$E[w_{t}^{2}(i)\vert F_{t}] \leq A+B\vert\vert r_{t}\vert\vert^{2}$](img57.gif) for some A,B constants.
for some A,B constants.
- 3.
- the steps
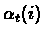 are such that:
are such that:
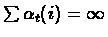 and
and
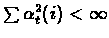
- 4.
- the mapping H (operator) is contracting
Then
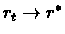
with probability 1 .
(where
R* is the fixed point of
Hr*=
r*)
In the case of Q-Learning it means that
HQ*=Q* and Q* is the optimal value
function,
(this is the same operator as in Value Iteration).
Thus we achieve by the convergence of Q-Learning the optimal policy value.
Theorem 9.2
If all r(s,a) are non-negative and bounded and
Q0(
s,
a)=0 then
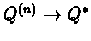
For the theorem to be true we assumed that we sample each (s,a) infinite number of times,
thus we could look at each sequence separately.
How to assure that we visit all (s,a) ?
- 1.
- If we follow the greedy policy of Q(n) it may be not possible to check all pairs
(s,a)
even if we reach all states 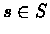
- 2.
- We will follow from a state s the
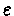 -greedy policy. With probability
-greedy policy. With probability
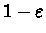 we choose the greedy action from s,
we choose the greedy action from s,
and do a random policy from s with probability
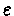 .
.
- 3.
- Choose the policy by:
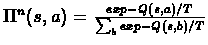
T determines if we do
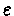 -greedy action (T
-greedy action (T
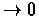 )
or random action (T
)
or random action (T
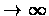 ).
We can look at this as if we part the time into sections of explorations(random) and of
explotation(greedy).
).
We can look at this as if we part the time into sections of explorations(random) and of
explotation(greedy).
On all 3 methods we can decide if we want to exploit the knowledge we have or get more
information about the MDP
The next theorem is a weaker version of the main theorem.
Theorem 9.3
Let
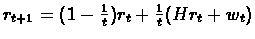
Assume that:
- 1.
-
E[wt]=0 and
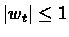
- 2.
- H is a contracting mapping
- 3.
-
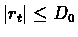
Then
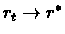
such that
Hr* =
r*
Proof:Since H is contracting,
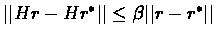 for some
for some  .
.
Whithout loss of generality, assume that r*=0,
therefore
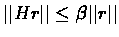 .
.
Define:
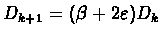 such that
such that
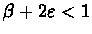 .
.
We show by induction that exists a time tk such that for every
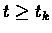 then
then
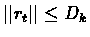
We bound rt for t>tk.
since
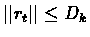 then
then
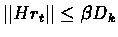 (the induction
hypothesis).
(the induction
hypothesis).
We have:
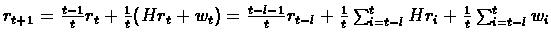 .
.
choose l=t-tk then :
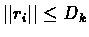 and
and
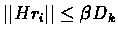 .
.
Since
E[wi]=0 and
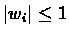 we have that:
we have that:
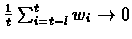 .
Therefore
.
Therefore
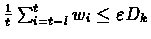 for all but a finite
number of t.
for all but a finite
number of t.
We continue:
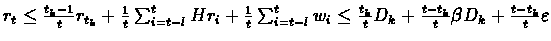
For
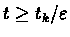 we get:
we get:
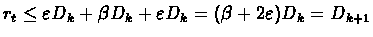
Therefore exists tk+1 such that
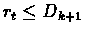
Thus when
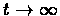 then
then
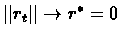 .
.




Next: About this document ...
Up: No Title
Previous: SARSA
Yishay Mansour
2000-01-07
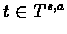
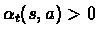
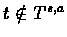
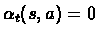
![]() for some
for some ![]() .
.
![]() .
.
![]() such that
such that
![]() .
.
![]() then
then
![]()
![]() then
then
![]() (the induction
hypothesis).
(the induction
hypothesis).
![]() .
.
![]() and
and
![]() .
.
![]() we have that:
we have that:
![]() .
Therefore
.
Therefore
![]() for all but a finite
number of t.
for all but a finite
number of t.
![]()
![]() we get:
we get:
![]()
![]()
![]() then
then
![]() .
.
![]()