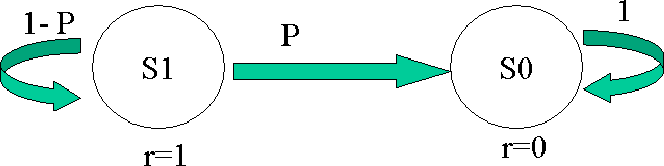
Consider the MDP in the Figure 7.1. Let N be the length of the run.
We choose
![]() (undiscounted).
It is easy to see that,
(undiscounted).
It is easy to see that,
![]() ,
,
since the distribution is geometric ("success" with probability p when
moving to s0). However note that
![]() , which implies that
r(s1,T,j) are independent.
, which implies that
r(s1,T,j) are independent.
The return from the k-th appearance of S1 until the end of the run is
N-k (there are N steps in the run, each of them with reward 1 and the run
ends the first time we get to S0).
The average is
![]()
Hence
![$E[\frac{N+1}{2}]=\frac{\frac{1}{p}+1}{2}=\frac{1+p}{2p}$](img104.gif) .
.
Note that this is different from
![]() .
.
The difference (bias) is because the random variables are dependent.
Error Calculations
The fact that Every Visit is biased does not implies that it is inferier to First Visit ,
as an estimate. Consider using a single run to estimate the return in the above example.
- First Visit :
![$Var(\hat{V_{F}}(S_{1}))=E[N^{2}]-E^{2}[N]=\frac{1}{p^{2}}-\frac{1}{p}$](img106.gif)
Note that the variance in this case can be bigger than the expected value when p is small. for example if p=0.1 then the expected value is 10 and variance is 90. - Every Visit :
![$E[(\frac{N+1}{2}-\frac{1}{p})^{2}]=$](img107.gif)
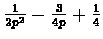
![]()
![]()
![]()
Next: About this document ...
Up: Evaluating Policy Reward
Previous: Every Visit
Yishay Mansour
1999-12-16