


Next: About this document ...
Up: Large State Space
Previous: Approximate Value Iteration
Example
Figure:
Example 2 Diagram
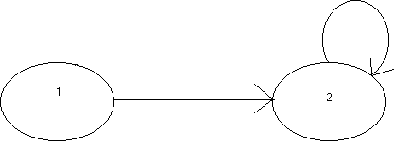 |
We will show a MDP, where the approximate value iteration does not converge. Consider an approximation 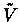 such that,
All the rewards equal zero. Therefore V(1) = V(2) = 0
such that,
All the rewards equal zero. Therefore V(1) = V(2) = 0
One can see that for r = 0 we have the value function. We calculate the square error, and choose the r that minimizes it.
In this simple case the minimum can be easily computed. We have,
The derivative is,
Hence, the minimum is at
Since
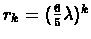 for
for
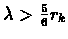 we have thatrk diverges.
We have shown an example for a value function, which does not converge.
We will look to see if our assumption was not satisfied
we have thatrk diverges.
We have shown an example for a value function, which does not converge.
We will look to see if our assumption was not satisfied
The error is a function of rk and therefore we do not have an upper bound and the assumption is not satisfied.
Yishay Mansour
2000-01-11
