Answer to the Question 09/99
MEAN DEFLECTING FORCEThe question was:
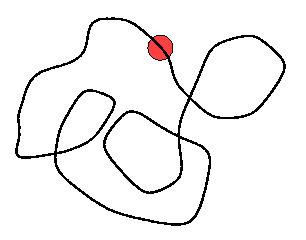
Consider a bead sliding without friction on a wire placed in a horizontal plane and forming a closed loop. The force acting on the bead is always perpendicular to the direction of its motion, to the right or to the left depending the direction the wire is curving. A force to the right or to the left, relative to the direction of the bead's motion, is defined as positive or negative, respectively. Let the mass of the particle be m and its (constant) velocity v, while the length of the wire loop is L.
(a) If the loop doesn't intersect itself, what is the time average of the perpendicular force, and how does it depend on the shape of the loop?
(b) What if the wire does cross itself? (This means that parts of the loop are slightly out of horizontal plane.)
(9/99-2/00) The problem has been solved by Andrew Wiggin (e-mail awiggin@hotmail.com) (his solution is presented below), by Christian von Ferber from University of Duesseldorf in Germany (e-mail ferber@thphy.uni-duesseldorf.de), by Baruch Meerson from Hebrew University in Jerusalem (e-mail meerson@domain.fiz.huji.ac.il), by Jhinhwan Lee a Ph.D. student at Center for Science in Nanometer Scale at Seoul National University, Korea (e-mail jhinhwan@csns.snu.ac.kr), and by Sumit Banerjee from Indian Institutes of Science and Astrophysics (e-mail sumit@iiap.ernet.in).
The answer:
The mean deflecting force for non-self-intersecting loop is 2{pi}m*v2/L, - just like for a circle. It does not depend in the details of the shape.
For a general figure the prefactor 2{pi} should be replaced by the total angle by which the direction of bead motion was rotated.
The solution:
First we assume that the loop has no crossings. The positive/negative direction of the force depends on the positive/negative curvature radius R, corresponding to deflection to the right/left. The instantaneous acceleration is always
a = v2/R = F/m
Since the speed is constant, change in the velocity dv directly maps into the deflection angle d(theta).
a dt = dv = v d(theta)
Hence, integrating
Fav = 1/T int[F dt], where T = L/v
trivially gives that the average force depends only on the total deflection angle, delta(theta)
Fav = (m v2/L) delta(theta)
For a simple loop delta(theta) = +/- 2{pi}. So ignoring the overall sign, Fav = 2{pi}m*v2/L, same as for the circle.
In (b), one needs a careful evalution of the total angle by which the velocity was rotated. It is quite obvious that this will be |delta(theta)| = 2{pi}*N, where N is an integer that tells how many complete turns are made by the loop. It has to be determined from the geometry of the loop.
We do not know a simple rule relating the total angle of rotation and the shape of the curve. (Of course, one can simply integrate the d(theta) and find the angle analytically.) There are some simple relations: e.g., if the number of self-intersections of the projection of the curve is even (odd), then the total number of rotations is odd (even). Unfortunately, this is insufficient... We received many suggestions how to calculate the number of rotations. The suggestions, were either as complicated as direct evaluation of the angle by "following the curve" or they included poorly-defined rules which needed to be refined every time a more complicated shape was considered.
 Back to "front page"
Back to "front page"