Answer 07/99

Answer to the Question 07/99

MISSING ENERGY

The question was:

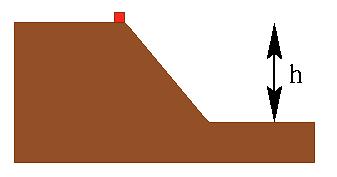A body starts sliding (from rest) without friction down a hill of height h. In the beginning the body has potential energy and no kinetic energy; at the end the body has only kinetic energy. It follows from energy conservation, mgh=½mv², that the velocity of the body at the bottom of the hill will be v=(2gh)^1/2.

Now consider the same process from a reference frame moving with velocity v (to the right) relative to the ground. In this reference frame, the body in the beginning has potential energy mgh and kinetic energy (1/2)mv², while at the end of the process both energies vanish. Where did the energy disappear? Give a detailed account of missing energy!

(7/99-11/99) The problem has been solved by Gerrit Danker (e-mail Gerrit.Danker@student.uni-magdeburg.de), by Fernando Ferreira (e-mail ferreira@mercury.ubi.pt), and by Adi Armoni (e-mail Adi.Armoni@cpht.polytechnique.fr).

The solution:

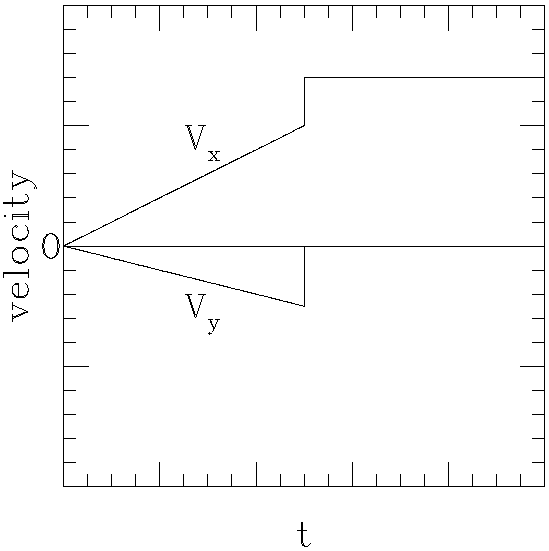
Before we begin the solution it is important to understand several basic facts about this problem. [At the very end we will present a solution of a more general problem, but we start with the problem in the form in which it was posed.] The following figure depicts the horizontal and vertical components of the velocity in the reference frame of the ground. Both velocities are linear functions of time t as long as the body is on the slope. However, when the body reaches the bottom of the hill the direction of its velocity suddenly changes. At that moment there is no change in the magnitude of the velocity, but both vertical and horizontal components change suddenly.

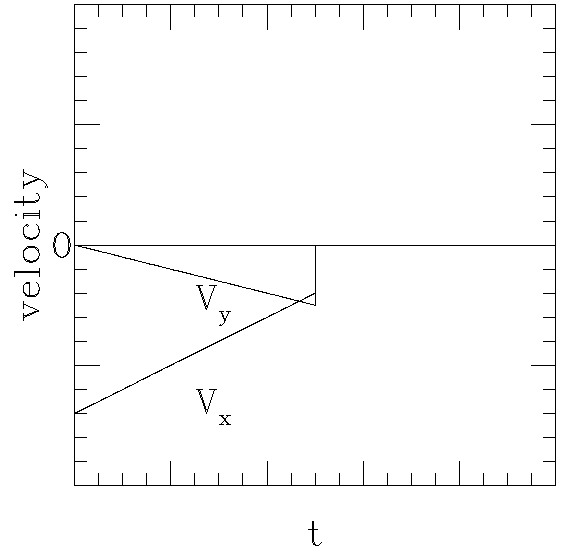
Now let us look at the same events from the reference frame which moves relative to the ground with velocity v to the left. In this reference frame, the discontinuities in the velocity components are still present, and therefore the total velocity undergoes a sudden change from a finite value to zero, when the body reaches the bottom of the slope and goes into the horizontal plane. Clearly, in what follows we will need to consider both what happens on the slope and what happens at the last moment of the slide - during the transfer from the slope to the horizontal plane.

In the moving frame of reference the initial energy of the body is mgh+½mv²=2mgh. All our calculations will be performed in the moving frame of reference. In this frame (which moves with velocity v relative to the ground) the body is no longer moving in the direction parallel to the direction of the slope of the hill. Nevertheless, we can consider the components of the velocity which are parallel and perpendicular to the slope. Since the body remains in contact with the slope, its velocity perpendicular to the slope does not change, and therefore there is no acceleration in that direction. Therefore the component of the weight mg cos A, where A is the angle of inclination of the hill, is compensated by the normal force of equal size (and opposite direction). The acceleration of the body in the vertical direction is a=g-g cos² A=g sin² A, which is the difference between the weight and the vertical component of the normal force of the hill divided by m. Since the vertical component of the initial velocity vanishes, the time required to travel from height h to the bottom of the hill is

t=sqrt{2h/a}=sqrt{2h/(g sin² A)}.

The work performed by the normal force of the hill will be equal to its product with the distance that the body travels in direction perpendicular to the slope of the hill (with velocity v sin A). The distance traveled by the body in the direction perpendicular to the hill is v sin A t=v sqrt{2h/g}. Thus the work performed by the hill on the body is:

W₁=-mg cos A v sqrt{2h/g}= -2mgh cos A.

Note that this work depends on the slope and does not compensate for all of the energy loss 2mgh, i.e., the body reaches the bottom of the slope with kinetic energy 2mgh(1-cos A). This, however, is not the end of the story. At the very bottom of the slope the body moves from the slope to the horizontal plane. For a very short time it moves on a highly curved path. In the reference frame of the Earth, this last stage modifies the momentum, because the direction of motion changes; however, the energy remains unchanged. In the moving reference frame, work is performed by and on the body during this last stage of motion.

There are several ways to calculate the work performed on the body at this last stage. A clear intuitive understanding of the process can be obtained if one replaces the sharp corner (the transition between the slope and the horizontal plane) by an arc of a small circle which interpolates between the slope and the horizontal plane. The angle of the arc as viewed from the center of that circle is A. Now one needs to evaluate the work performed on the body while it moves along the arc. Of course, the force depends on the radius of curvature R of the arc, but the final answer does not depend on that radius.

By analyzing the motion of the body in the moving reference frame, it can be shown (we do not give the explicit derivation) that the force that the surface applies on the body is given by mU²/R, where U is the velocity in the reference frame of the Earth. Moreover, the reader can convince himself that U does not change during the motion along the arc and is equal to v, although in the moving reference frame the velocity decreases with time. When the radius vector drawn from the center of curvature to the position of the body changes its angle B from the vertical by dB, then the work performed on the body is mv²sin B dB. As angle B changes from A to 0, by integrating the expression for the work we find that the total work performed is exactly -2mgh(1-cos A), i.e., it eliminates the remaining energy of the body. In this paragraph we did not actually calculate the work performed on the arc, but only indicated how it can be done.

All the above remarks were somewhat specific to the given shape of the hill. Adi Armoni solved the problem for a hill of any shape. The postscript file of his solution is HERE. Note that his solution is very general. Read it and compare with the solution for the particular shape of the hill presented above.

Back to "front page"