Answer to the Question 12/98
COUPLED PENDULUMSThe question was:
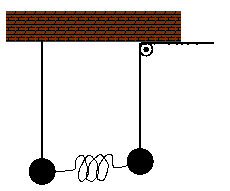Two pendulums with equal masses m
are coupled by a spring with spring constant k
as shown in the figure. Length of the left pendulum is l,
while the length of the right pendulum is different: l+x.
The length of the right pendulum can be varied. Assume that at the initial
moment the right pendulum is shorter than the left one (x<0).
We deflect
the left pendulum and release it. The system starts oscillating. Now we
gradually increase the length of the right pendulum until it is
longer than the left one. How will the system behave at the end of
this process?
(12/2003) The problem has been solved correctly by Sergei Flach from Max Planck Institute for the Physics of Complex Systems, Dresden, Germany (e-mail flach@mpipks-dresden.mpg.de) almost immediately after publication of the problem (12/98). We expected that this problem will generate many attempts at the solution, but recieved only few partial solutions. John G. Florakis, a Physics student at the University of Athens (Greece) (e-mail sniper_700@hotmail.com) came (7/2003) very close to the desired solution. After 5 years, it seems that we should publish the solution. Flach's (slightly editted) solution is presented below.
The solution:
There is an ambiguity in the problem, because the system is nonlinear and nonintegrable, so in general an irregular motion is generated, with any outcome you wish. But I assume that the pendula are weakly excited, and therefore we can linearize the equations of motion. Further I assume that 'gradually' means adiabatically slowly, i.e. when we solve at any fixed length l+x, the eigenvalue problem and prepare the system in a mixture of the two possible eigenstates (f1,f2) c1*f1+c2*f2 where f1,f2 are the eigenstates and c1,c2 are the weight factors, then upon changing the length l+x we do not change c1,c2, but simply gradually change f1,f2. Due to the nonzero coupling we generically won't run through a degeneracy (eigenvalues e1,e2 are different for all x), what we find is an avoided crossing, i.e. for weak coupling e1(x) and e2(x) will come very close if x=0. Simple calculation of the tuning of a 2x2 matrix by a parameter close to a degeneracy shows that after the avoided crossing f1 --> f2 and f2 --> -f1. This implies that after the crossing (after the change of sign in x) the system is in a state c1*f2 - c2*f1.
Suppose that when at the beginning x was positive, our initial condition was such that that the solution was not permutational invariant (i.e. e.g. one oscillator oscillates with large amplitude and the other one with small amplitude). That can in general happen because nonzero x breaks permutational symmetry. Now after the experiment x --> -x and consequently now we have the permuted solution - i.e. the right oscillator is having large amplitudes, while the left one does not.
w2=sqrt[0.5(g/l1+g/l2+2k/m) +- sqrt[0.25*(g/l1-g/l2)2+(k/m)2]]
The graph is for the case when (k/m)=0.05(g/l2).
Back to "front page"