Discussion of the Question 06/98

The question was:

Stanislav Ulam asked (in "The Scottish Book") whether a sphere is the only solid of uniform density which will float in water in any position. We ask a simpler, two-dimensional, question: Consider a long log of circular cross-section; it will, obviously, float in any position without tending to rotate. (Of course, the axis of the log is assumed to be parallel to the water surface.)

(a) Are there any additional cross-section shapes such that the log will float in any position if the density of the floating body is 0.5 gm/cm³?

(b) Are there any shapes for some other (predefined) values of the density? (Of course, we assume that the given density is smaller than the density of water.)

(c) Are there any shapes, besides the circle, which will float in any position independent of the density of the material?


Answers and solutions

PART (a)

(5/2000) Ch.v.Ferber:  It took some time, but finally part (a) of the problem has been solved by Franz Wegner from the Inst. für Theoretische Physik in Ruprecht-Karls-Universitat Heidelberg (e-mail wegner@TPhys.Uni-Heidelberg.de ). His elegant derivation can be found in the postscript file .

Outline:Wegner first proves a remarkable property of the `waterline', the line that the water level draws on the cross section of the log: This line divides the cross section in two areas, one above, one below the water level. For a log that solves the problem not only the areas above and below are constant, i.e. independent of the position of the log, but also the length of the waterline itself is constant.
This condition holds independent of the density of the log. For density 1/2 Wegner explicitly constructs curves that comply with this condition and shows that these indeed solve the original problem.

History: This problem (in response to Ulam's question) was originally solved by H. Auerbach. The solution was published in Studia Math. 7, 121-142 (1938) as cited in `The Scottish Book'. Auerbach for his solution he had reinvented curves that had been discussed by K. Zindler even before Ulam had posed his problem Monatsh. Math. Phys. 31, 25-57 (1921). Auerbach's solution, written in French and using a more geometrical approach, is equivalent in most part to that of Wegner. The only difference is that the condition for convexity as also suspected by Wegner is too restrictive. In fact one may allow the solution to be non-convex at some points, convexity `nearly everywhere' is enough. In this way the following shape is shown to be a solution:



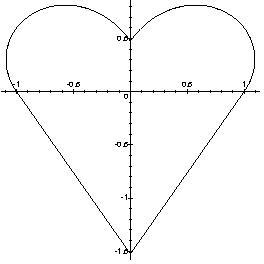
In Wegner's notation this corresponds to

s(phi)=cot(alpha+phi)	for	0<phi<pi/2
s(phi)=-cot(alpha+pi-phi)	for	pi/2<phi<pi	with tan(alpha/2)=0.54037..

PART (b)

(5/2000) Ch.v.Ferber:  We do not yet have a full answer to the part of the problem when density is not equal 0.5. However, it should be mentioned that the property of the `waterline' to be constant and to divide the shape at a constant ratio remains true as proven by Wegner. Auerbach furthermore proves the following condition to be necessary and sufficient: The waterline chord is constant and divides the perimeter into arcs of constant length. So it remains to be shown that the corresponding generalizations of the Zindler curves exist.

(5/2001) Y. Kantor: In 2/2001 we received a letter from Paul Erdos (e-mail pal.erdos@bluewin.ch) Professeur honoraire at The Institute of Theoretical Physics of University of Lausanne, Switzerland (not to be confused with the late mathematician Paul Erdos (1913-1996)). In his letter, Erdos pointed out that Auerbach, in his 1938 paper, suspected that for densities different from 0, 1/2 and 1 the shape should be circle. Auerbach noted that E. Salkowski claimed to have proved this property (in Sb. D. Heidelb. Acad. D. Wiss., Math.-nat (1934), 57-62) but admitted that he does not understand the proof. Erdos pointed out to us that Salkowski's proof is erroneous. Erdos also sent us his own (yet unpublished) proof that at for specific non-trivial, different from 0, 1/2, 1, densities the cross section must be a circle.

(5/2002) Y. Kantor: Recently (3/2002 and 5/2002) Franz Wegner from the Inst. für Theoretische Physik in Ruprecht-Karls-Universitat Heidelberg (e-mail wegner@TPhys.Uni-Heidelberg.de ) found equations (and shapes) of non-circular logs that will float in arbitrary orientations, for specific sets of densities. See details in the following papers in PDF format: 1 and 2.

PART (c)

(6/98) Y. Kantor:  Many people noted that part (c) of the question can be easily solved. Omer Edhan (e-mail edhan@netvision.net.il) was the first to answer correctly. Most of the solutions provided only a partial argumentation. The complete and correct argument for part (c) is as follows:

Since the question refers to floating body of arbitrary density it must be also correct in the limit of vanishing density. A body is in stable equilibrium when the difference between the height of the center of mass and the center of buoyancy (center of mass of the part which is under the water surface) is minimal. In the vanishing density limit, the center of buoyancy is at the water surface, and the question is reduced to minimization of the height of the center of mass. Since the body is supposed to be in equilibrium independently of its orientation the height of the center of mass must be independent of the orientation, and therefore the distance between the center of mass and the water must be independent of orientation. Therefore the external boundary of the cross section of the log must be a circle. (L. Montejano, proved this statement in Studies in Applied Mathematics 53, p. 243 (1974).) (Of course, one can also use a log with a hole - log of circular cross section from which a smaller concentric circle has been removed.)

(5/2001) Y. Kantor: In a letter by P. Erdos (see par.(b)) it was brought to our attention that H. Steinhaus proved (Bull. Acad. Poloaise des Sc. Math., Astr. et Phys. XI No.4 (1963) 173-174) that for a three dimensional body on a horizontal support must be a sphere with it center of gravity coinciding with the center of the sphere. So, L. Montejano essentially proves the same thing (in two dimensions) apparently unaware of Steinhaus' work.

Back to "front page"