Answer to the Question 02/98
A FLOATING TRIANGLEThe question was:
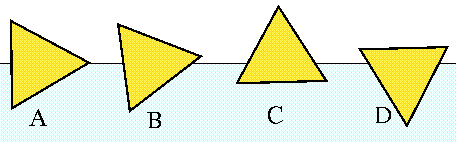
A wooden log (density 0.5 gm/cm3) is floating in the water. The cross section of the log is an equilateral triangle. Which side up will it float?
(3/98) Christian von Ferber (e-mail ferber@orion.tau.ac.il), a post-doc at Tel Aviv U., correctly solved the problem.
The answer is: The triangle will float as depicted in Fig. A, i.e one of its medians will be exactly at the waterline.
Here we present some main points of the solution.
Since the density of the body is half the density of the water, the waterline will divide the triangle into two halves. (If the density (relative to the water) is rho then only the fraction rho of the area of the triangle will be under water.)
The point of application of weight of the triangle is its center of mass (c.m.). One can easily convince himself that the c.m. of a triangle is at the intersection of the medians. The direction of the force of weight is vertical (down). The point of application of the Archimedes force is the center of mass of the underwater part of the triangle (center of buoyancy). Its direction is vertical (up) and its size is equal to the weight. At the equilibrium, the points of application of the weight and the Archimedes force must be exactly one above the other.
In order to determine the stability of the equilibrium it is convenient to look at the potential energy of the system which is proportional to
W=(vertical coordinate of the c.m.)-(vertical coordinate of the center of buoyancy)
A direct calculation of the quantity W shows that the system has minimum of energy at the position depicted in Fig. A, while the positions of a corner pointing up or down correspond to maxima of energy. Note that due to the symmetry there are 6 stable equilibrium positions.
If rho is NOT equal to 0.5, the equilibrium orientation depends on rho. Only a fraction rho of the triangle will be under the water. It is interesting to note that there is the is a relation between cases with density rho and 1-rho. In these cases the underwater and above-water parts of the triangle simply exchange roles.
For low densities [rho < (7/16)] the triangle will float his corner pointing exactly up as in Fig. C. (There are 3 such positions.)
For high densities [rho > (9/16)] the triangle will float his corner pointing exactly down as in Fig. D. (There are 3 such positions.)
At the intermediate densities [(7/16) < rho < (9/16)] the solutions are not symmetric, and the position of flotation is as in Fig. B. (There are 6 such positions.) The following figure depicts the rho-dependence of the angle between one of the sides of the triangle and the water surface.
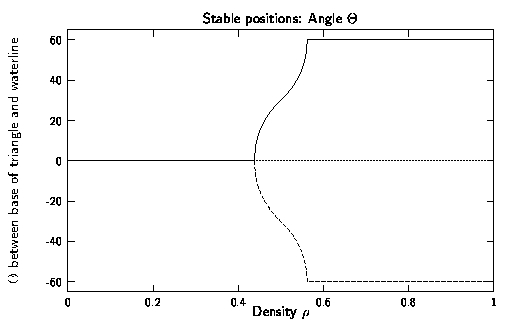
(5/2001) Y. Kantor: In 2/2001 we received a letter from Paul Erdos (e-mail pal.erdos@bluewin.ch) Professeur honoraire at The Institute of Theoretical Physics of University of Lausanne, Switzerland (not to be confused with the late mathematician Paul Erdos (1913-1996)). He has drawn our attention to his papers on "Floating equilibrium of symmetrical objects and the breaking of symmetry" [P. Erdos and G. Schilbler, Am.J.Phys. 60, 335 (1992) (Part 1), Am.J.Phys. 60, 345 (1992) (Part 2)]. In Part 1 of these papers the floating equilibrium for the current case of a triangular prism is treated in detail and in particular the above curve for the tilt angle as function of the density rho is derived. The same analysis for the square prism yields a similar result. The symmetry breaking behavior of floating symmetric bodies is observed in Part 2 of this study also for the cube, the octahedron and the tetrahedron.
 Back to "front page"
Back to "front page"