
Answer to the Question 04/05
LINEAR MOLECULES
The question was:
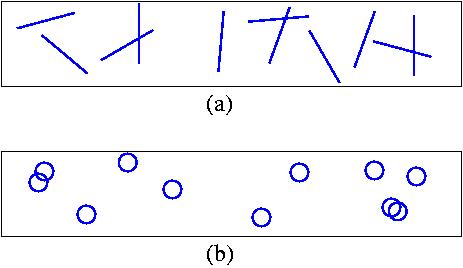
Consider a two-dimensional gas of molecules inside a rectangular
box of small width d and very large length.
If the box is filled by point-like molecules with density n,
then the pressure is p=nkBT.
(kB is the Boltzmann constant, and
T is the temperature.) If the point-like molecules
are replaced by thin linear molecules of length L, then
the pressure will slightly increase.
(a) Consider a case when L
is smaller (but not much smaller) than d,
and the molecules do not interact with each other, but they
cannot penetrate the walls of the box. (See picture (a).)
Calculate the exact pressure in the box.
(b) Consider a case when the molecules of lengths L
form rigid circles of diameter L/{pi}. (See picture (b).)
Calculate the exact pressure in the box.
(c) Note that your answers to (a) and (b) produced corrections
to the leading term (nkBT) that are simply
related to each other. What is the reason for that simple
relation?

(1/06) Y. Kantor: This problem is closely related to probabilistic question
that was asked by Georges-Louis Leclerc, Comte de Buffon (1707-1788), - Darwin's
predecessor in the area of evolution. The well known "Buffon's needle problem"
is beautifully described in Ch. 21 of the book by M. Aigner and G.M. Ziegler
"Proofs from THE BOOK", Springer, Berlin, 3rd edition (2004). Below we use results
from that book.
(1/06) This problem has been solved correctly (11/6/05) by
Chetan Mandayam Nayakar, a student at India Institute of Technology,
Madras, India
(e-mail mn_chetan@yahoo.com),
and in a more detailed form by Ioannis Florakis from the University
of Athens, Greece (e-mail iflorakis@yahoo.gr.
Florakis' solution can be found in the following PDF file.
The answer:
For circular molecules, pressure p=nkBT/(1-L/(pi*d))
and for linear molecules, pressure p=nkBT/(1-2L/(pi*d)).
The reason for such simple relation between the solutions is explained below.
The solution:
The detailed solution for both linear and circular configurations can be found
in PDF file of the solution of Florakis. This is
a relatively straightforward solution. One needs to calculate the statistical
sum, which requires calculation of the "volume" that can be occupied by a
single molecule in the space of two dimensions + the angle (direction of the
rod). In the case of a linear molecule it presents a relatively simple integral
leading to a solution mentioned above. In the case of circular molecule the
calculation is trivial, since the orientation of the circle become irrelevant.
The available volume in both problems can also be calculated as the entire
volume of the box multiplied by the probability that a straight line of length
L or a circle of such circumference is randomly dropped on a plane with
an infinite number of parallel lines separated by distance d without
crossing any of those lines. This is the probabilistic question of Buffon.
There is an apparent simple relation between the solutions of the problems.
We did NOT receive a simple (and/or elegant) explanation why this is so.
The explanations of the type "that is what you get by averaging over
angles of a linear molecule" are just a simple restatement of the answer.
There is a deeper relation here! And the answer is hidden in understanding
how are Buffon's problems for a circle and a line related!
Consider, say, four equal short straight segments thrown with random
orientation (and independently)
on a plane covered with infinite parallel lines separated
by distance d, as depicted in the Fig.(a) below. The expectation
value of the number of times that the segments cut infinite lines
(denoted E) is proportional to the number of segments. (I.e., in this
particular example it is equal the 4 times the expectation value for a single segment).
Now consider a case when the segments are connected into a single curve
with fixed angles between the adjacent segments. This curve is thrown
with random orientation on the plane as shown in the Fig.(b) below.

STATEMENT: The expectation value of the number of times the curve cuts the
infinite lines is E, i.e. the same number as in the case of independent
segments. This is true, because the expectation value of a sum (of numbers of
intersections by each small segment) is equal
to the sum of expectation values even when the variables are correlated.
Moreover, this statement is independent of the shape of the curved
line. Thus, the same answer is obtained by a straight line and by a curved
line. In particular, if we throw a straight line of length L, and a
circle of perimeter L, the expectation value of the number of
intersections is the same. If L is smaller that d, then
the straight line can only have 0 intersections or one intersection, and
E is simply equal to the probability of having one intersection.
In the case of circle, it can have 0 intersection or two
intersections with straight lines. The expectation value
E is is equal to two
times the probability of the circle intersecting a line. Consequently,
the probability of circle intersecting a line is half of the
probability of straight segment intersecting a line. This
explains the factor 2 in the corrections to pressure.
 Back to "front page"
Back to "front page"




 Back to "front page"
Back to "front page"