Answer to the Question 11/01
RESISTOR NETWORKSThe question was:
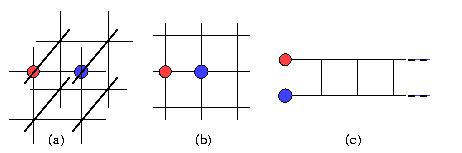
Consider and network built of wire segments having unit resistance. Find the resistance between two adjacent nodes of the network (denoted by blue and red in the figures) if the network is:
(a) infinite simple cubic network;
(b) infinite square network;
(c) semi-infinite "ladder".
(3/02)The problem was solved correctly by many people. Loic Turban from Universite Henri Poincare (Nancy, France) (e-mail turban@lpm.u-nancy.fr) both solved (19/12/01) the general case of z-coordinated periodic lattice, and suggested addition solvable geometry (see below). Predrag Lazic a Ph.D. student in Zagreb, Croatia (e-mail predrag.lazic@zg.tel.hr) both solved (26/1/2002) the proposed questions and suggested an additional solvable geometry.
Answer: (a) 1/3; (b) 1/2; (c) 1+sqrt{3}.
The solution:
(a) and (b) Square, cubic and general hypercubic lattices in D space dimensions can be solved as follows:
Assume that current I is inserted from outside into the "red" junction and withdrawn at infinity. Since the system is symmetric around the injection points the current will split equally into 2D currents in bonds connected to the junction. In particular, along the bond connecting blue and red junctions there will be current I/(2D).
Now consider a different situation: current I is removed from blue junction and is injected from infinity. At each of the bonds entering the blue junction, there will be a current I/(2D).
Now consider a linear superposition of two above situations: Current I is injected into the red junction and current I is withdrawn and the blue junction, and nothing happens at infinity. The current on the bond connecting the red and blue junctions will be I/(2D)+I/(2D)=I/D. Therefore, the voltage between the junctions will be V=I/D, and consequently the effective resistance will be R=V/I=1/D. Thus, the resistance will be 1/3 for cubic, and 1/2 for square lattice.
(c) Assume that the resistance of the semi-infinite ladder is R. Then we can view the system as consisting of three unit resistors, when in parallel to the center resistor we connected an effective resistor R, as depicted in the following figure:
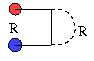
From simple sequential/parallel resistor rules we find:
R=2+1/(1+1/R)
which can be solved and gives R=1+sqrt{3}.
There are additional analytically solvable infinite networks. E.g., consider the following triangular network:
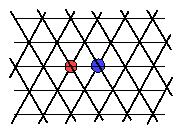
It can be solved in the same way as the square network. Convince yourself that the resistance between adjacent sites is 1/3. In general, if coordination number (number of nearest neighbors of a site) on a periodic (symmetric) lattice is z, then the resistance will be 2/z. E.g., for honeycomb lattice, z=3, and the resistance will be 2/3.
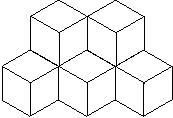
Loic Turban suggested to look at the resistance between the points of a honeycomb lattice separated by two bonds. If current I is inserted a point A then current (1/3)I will flow in a bond connecting A with its nearest neighbor B. That current will split, and (1/6)I will flow from B to next-nearest-neighbor C. The voltage drop between A and C will be (1/2)I. Similar argument can be repeated for current I being extracted from C; however, this time there will be current (1/3)I in BC, and (1/6)I and AB. Superposing two cases, we get current I inserted at A and removed at C, causing voltage drop of I, and consequently the equivalent resistance is unity. Similar "symmetry arguments" can prove that the resistance between second neighbors in a diamond lattice is 2/3. Also, one can show that the second neighbor resistance in a dice lattice is 1/2. The dice lattice is a two-dimensional lattice (despite its "3D appearance") shown in the following figure:
Predrag Lazic suggested to look at the resistance between the points of Sierpinski gasket. This geometry is obtained by iterative procedure. There are many simple fractal geometries that can be solved.
 Back to "front page"
Back to "front page"