Answer to the Question 02/01
LIMITED PENDULUMThe question was:
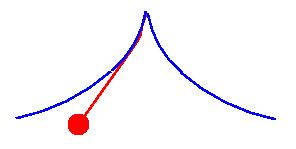
Period of a pendulum depends only on its length only for very small oscillations. For large oscillations the period depends on the amplitude. Such amplitude-dependence can be eliminated by making the string of the pendulum (shown in red) to rap around a limiting curve (shown in blue). What is the shape of this curve?
(6/2001) An elegant and short solution of the problem has been submitted (28/4/2001) by Szabolcs Galambosi a Ph.D. student at Department of Physics at University of Helsinki (e-mail galambos@pcu.helsinki.fi)). Derivation of the equation of motion below, closely follows his solution. [Arvind Murugan from Caltech (e-mail arvind@its.caltech.edu) pointed out (11/2/2001) that this is a well known problem solved by Huygens and it initiated the study of involutes and evolutes. We received some correct answers but no detailed solutions from several people (Itzhak Shapir (e-mail ishapir1@netvision.net.il), Chethan Krishnan (e-mail chethan@physics.utexas.edu))]
Answer: The curve is cycloid.
The solution:
DEFINITIONS
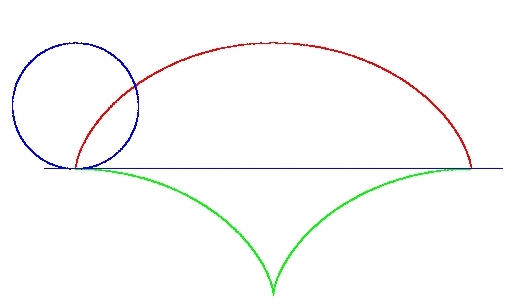
Cycloid (ordinary cycloid) is the locus of a point of a circle that rolls along the straight line.
Thus, if the blue circle in the above picture rolls along the horizontal line and in its leftmost position a point has been marked on its lowest part, then that point will trace the red cycloid. (Cycloid was first studied by Cusa, and later was properly defined by Mersenne in 1599. Galileo also studied this curve and gave it its name. Roberval found that the area below the cycloid is 3{pi}R2, where R is the radius of the circle.) The equation of cycloid is:
x=R[f-sin(f)]
y=R[1-cos(f)]
where f is the angle by which the generating circle has been rotated.
Evolute is a curve defined by the loci of the centers of curvature of a given curve.
Involute is a curve traced by a point on straight line rolling without slipping along a given curve. Involution is the inverse operation of evolution.
There are two curves (cycloid and logarithmic spiral) whose involutes are exactly the same curves. Evolute of the red cycloid above is the green cycloid, and, consequently, the red curve is the evolute of the green curve! We do not prove these properties (they can be found in books of analytical geometry). We will use those properties below.
PHYSICS
Now consider the above picture inverted (upside down), so that the heigh h=-y. A bead of mass m sliding along a cycloidal curve (the inverted red curve) will have potential energy change (relative to initial height ho): mg(h-ho). This decrease in potential energy should be equal the kinetic energy:
(1/2)mv2=(1/2)m[(dx/dt)2+(dy/dt)2
=mR2[1-cos(f)](df/dt)2
From the equality between the loss of potential energy and the kinetic energy we find:
dt=[(R/g)(1-cos(f))/(cos(fo)-cos(f))]1/2df
where fo is the value of the angle (of the generating circle) corresponding to ho. This equation can be integrated from f=fo to f={pi} to give the time of quarter period (time from uppermost point to lowermost point). Direct integration shows that this integral is independent of fo!!! The oscillation period comes out to be identical with the period of of small-amplitude oscillations of regular pendulum of length 2R. Thus the period of the bead sliding on an (inverted) cycloid is independent of the amplitude.
Szabolcs Galambosi suggested an alternative proof of time independent behavior. He suggested to form Lagrangian L=T-U from the kinetic energy T and the potential energy U that have been calculated above. Everything in this Lagrangian will be expressed in terms of f and its first time derivative f'. The resulting Euler-Lagrange equation will be:
2f"Rcos(f/2)-sin(f/2)f'2+g sin(f/2)=0,
which after a substitution a=Rsin(f/2) becomes
a"+(g/2R)a=0,
which is a simple harmonic equation for a, corresponding to a small-oscillations-pendulum of length 2R.
Now consider a bead hanging on string of length 2R. If its swinging is limited by the green cycloid (see picture above - inverted) then the bead will trace out a curve which is involute of the green cycloid, i.e. it will move along the red cycloid. Consequently, the period of such pendulum will be independent of the amplitude.
This property (that is called tautochrone or isochrone) was discovered by Huygens in his Horologium Oscillatorium in 1673.
(4/2004): A very straightforward and short solution of the problem has been suggested (16/4/04) by Sebastian Popescu (e-mail seba@uaic.ro) from Complex Systems Group in the Faculty of Physics of "Al. I. Cuza" University, Iasi, Romania. The solution can be found here.
(12/2004): A very interesting additiona has been provided (17/12/04) by Ioannis Florakis (e-mail iflorakis@yahoo.gr) from University of Athens, Greece. He has shown that harmonic oscillator (in one dimension) and cycloid (in two dimensions) are the only possible symmetric isochrone solutions of the problem. His discussion of the problem can be found here.
 Back to "front page"
Back to "front page"