The Cohen group at Tel Aviv University develops computational and theoretical methods for studying many-body quantum systems in and out of equilibrium.
Our group investigates nonequilibrium phenomena in chemical and condensed matter physics. We try to understand how strongly correlated quantum systems react to dissipative environments and to external perturbations, particularly in the context of the transport properties of nanosystems. This is a deeply challenging and fundamental problem, and we therefore work on state-of-the-art computational methods such as quantum Monte Carlo algorithms. Our specialty is cases where other algorithms fail due to sign problems, and we've developed techniques like inchworm Monte Carlo to overcome these challenges.
Learn more
Experimentalists can trap single molecules between metal leads, apply a (nonequilibrium) voltage across the junctions, and measure currents. We develop theories for understanding this complicated quantum process.
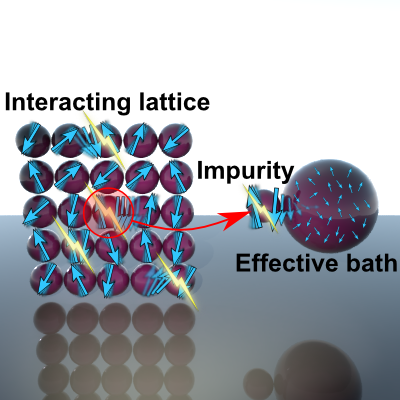
Big, strongly interacting quantum systems are among the most notoriously difficult problems in any field of science, but we can take advantage of an approximate mapping to relate them to simpler impurity models and junctions.
We work on various kinds of stochastic algorithms designed to study nonequilibrium systems and dynamical properties in strongly correlated systems, addressing both fundamental scientific issues and practical materials science questions.
We are a theoretical and computational research group with interests spanning chemistry and physics. Some of the common threads tying our work together are briefly introduced below.

One of the greatest fundamental challenges faced by modern theoretical science is the description of the nonequilibrium dynamics of strongly correlated quantum many-body systems. The essence of the difficulty with strongly correlated physics is that single-body approximations suitable to weak correlation (such as most electronic structure methods) do not work: the size of the Hilbert space needed to obtain accurate results increases exponentially with the system size. However, in the theoretical treatment of ground-state and equilibrium properties, many simplifications occur and a variety of efficient algorithms now exists. For instance, Density Matrix Renormalization Group (DMRG) takes advantage of the fact that in 1D systems, only an exponentially small fraction of the Hilbert space is important for representing low-lying states. Another example is Quantum Monte Carlo (QMC) algorithms, which can access finite temperature (and in certain cases even zero temperature) properties of systems by very efficiently performing propagation in imaginary time.
In nonequilibrium systems, no such simplifications are known to exist, and one is faced with the need to confront the full complexity of the problem. Analytical results and reliable approximations are limited to very specific regimes, and numerically exact results are therefore particularly important. We work on numerically exact solutions of simple toy models for quantum transport, called impurity models. These models let us account for the presence of strong correlations due to electronic interactions and coupling to vibrational degrees of freedom or optical modes. To apply QMC to nonequilibrium impurity models, time propagation must be carried out in real time, a fact which leads to a troublesome dynamical sign problem which severely limits the range of accessible timescales. We have shown that by combining bold-line QMC methods with reduced dynamics techniques, we can sometimes circumvent the dynamical sign problem, allowing us to gain access to slow spin relaxation dynamics within the Kondo regime. Using our recently developed inchworm Monte Carlo methods, we can completely bypass the dynamical sign problem in a wide variety of strongly correlated parameter regimes.


An exciting development in the study of extended correlated systems is Dynamical Mean Field Theory (DMFT), which defines a mapping between large or infinite systems where electrons interact on all sites and imourity models. This mapping only becomes exact in the rather unrealistic limit of infinite dimensional systems, but can be used as an approximation in 1D, 2D or 3D systems, where it turns out to capture many of the effects associated with strong correlation. The DMFT approximation can be systematically lifted (at greater computational cost) by considering multi-site impurity models. The most technically challenging part of DMFT involves solving for correlation functions in the impurity problem, which must be obtained at a very high level of accuracy to generate reliable results. In particular, in order to access dynamical information without the need for analytical continuation (which is effectively an uncontrolled approximation), the impurity problem must be solved in real time or real frequency, rather than within the computationaly easier imaginary time approach taken by most QMC methods. We applied the real time bold-line QMC method to correlation functions, showing that they could be accessed even within the strongly correlated regime.
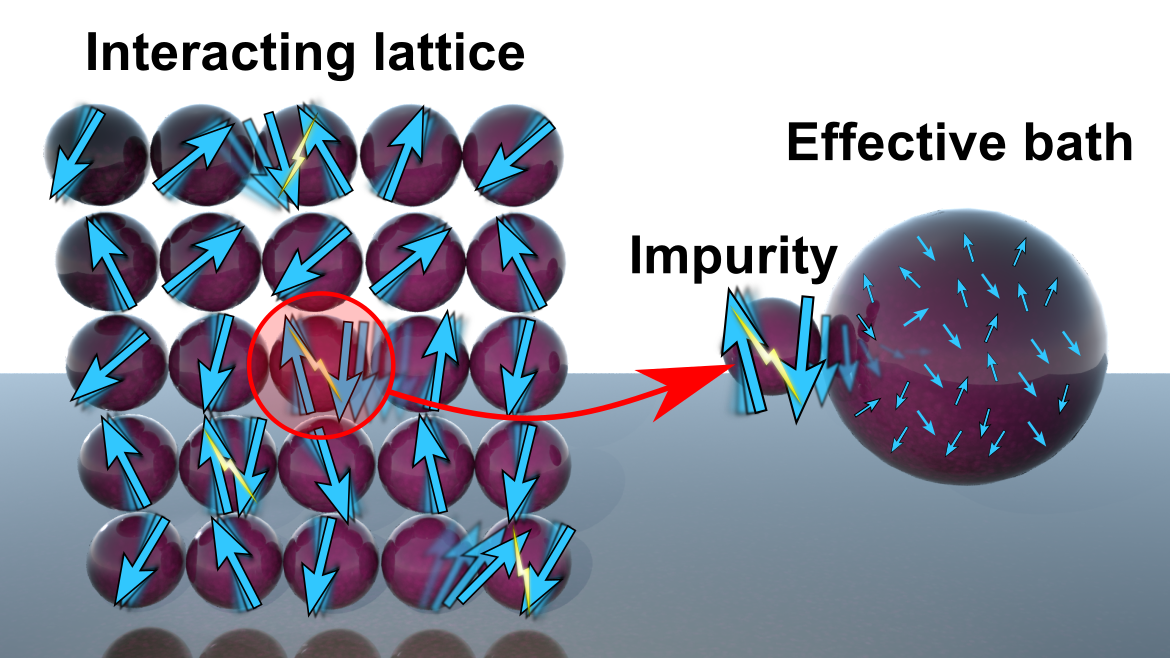
Nonequilibrium effects are particularly important at the nanoscale, since nanosystems are far easier to drive away from equilibrium than their bulk counterparts. Nanoscale and mesoscale physics is particularly challenging, because it deals with systems too big to be accessible to quantum chemistry methods and too small for approximations appropriate to the bulk to be valid. We are exploring DMFT approaches to correlated nanosystems ranging from molecular magnets on surfaces to transition-metal clusters in junctions. Strongly correlated systems in equilibrium display a remarkable variety of electronic phases, and a small change in pressure or temperature can take them across a phase boundary from metallic (or even superconducting) to insulating. We will address nanoscale, nonequilibrium issues: how do these systems respond to currents, laser excitations and rapid changes in external parameters? Can they be controlled?
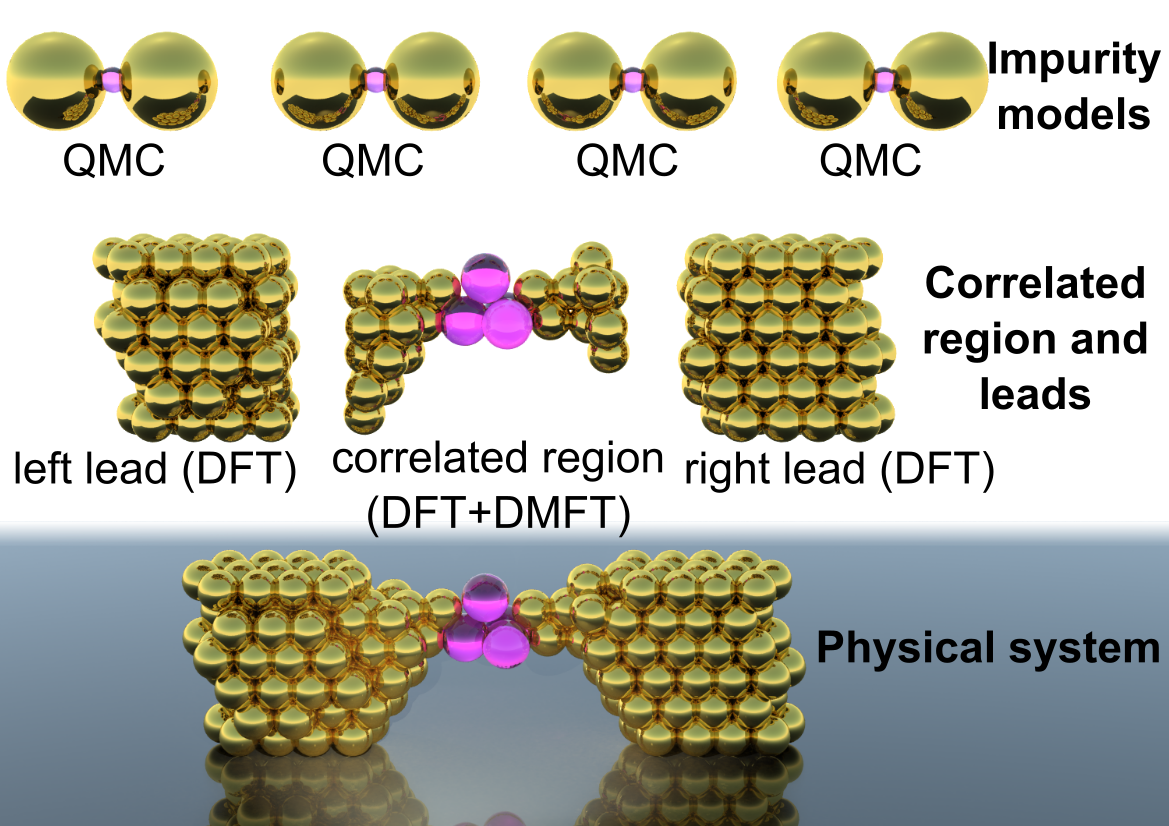
We also work on device applications and design criteria. There is tremendous interest in developing designs based on materials like transition metal oxides and dichalcogenides, which exhibit strongly correlated physics that established electronic structure theories fail to capture. Some of these materials are of interest because they are semiconductors with a 2D graphene-like structure; others because they display switching behaviors associated with metal-insulator transitions. Switching is at the heart of almost any application: devices which respond to their environment can be useful. To consider devices, one must evaluate properties like switching rates and energy efficiency; a nonequilibrium theory is therefore essential.
It is expected that when semiconductor devices are scaled down to the single-nanometer regime, the low number of carriers (which come only from a tiny percentage of dopant atoms) will result in problems associated with shot noise. One big advantage of correlated material devices is that we expect them to be scalable down to the single-nanometer regime, since a large fraction of electrons participates in the switching behavior.
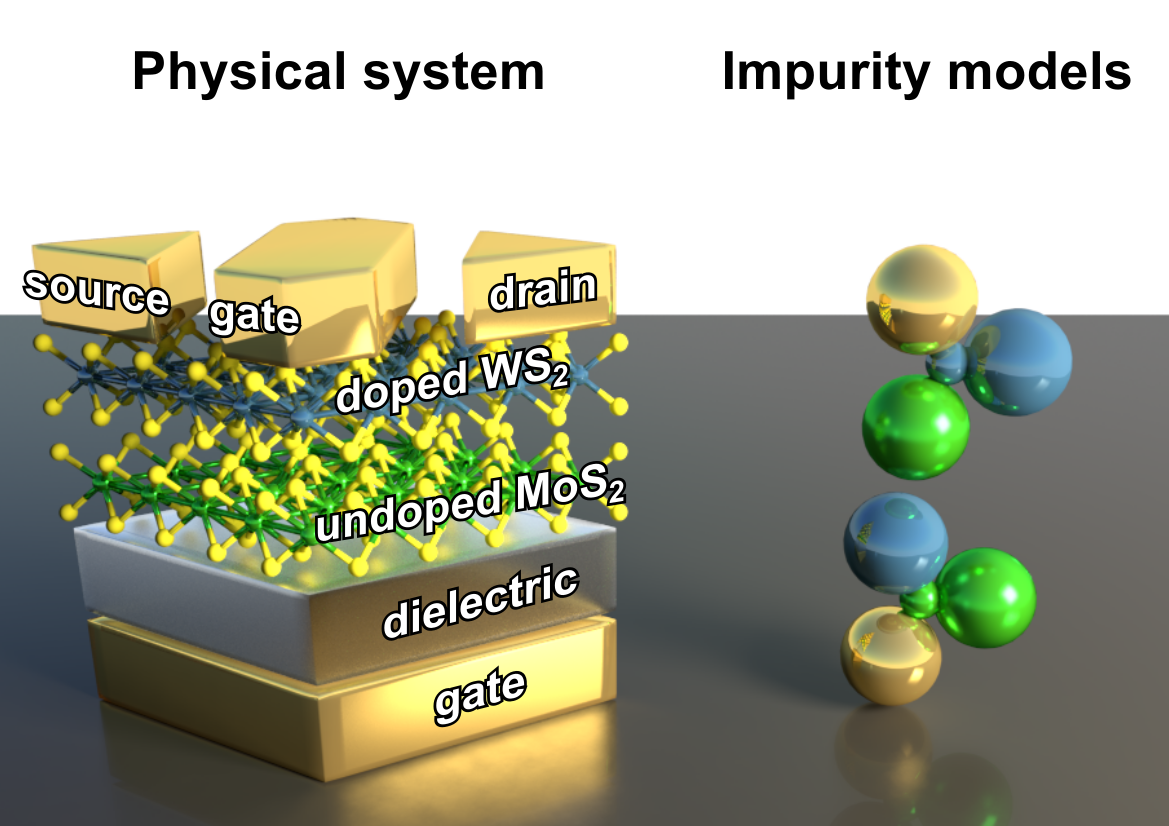
An almost universal aspect of electronic devices is the presence interfaces. Diodes, transistors and solar cells are all similar in that the key to their operation is the action at the inteface between pairs of different semiconductors. Strongly correlated materials exhibit even more interesting effects at their interfaces: for instance, metallic layers can form where two insulators meet. While similar 2D electron gases can form between semiconductors, here not only carriers donated by dopants participate, and the effects might therefore be expected to be far stronger and richer. We will investigate the dynamical properties of interfaces and their response to nonequilibrium forces.










B.Sc. - King's College London
Ph.D. - Imperial College London
Home page
B.Sc. - Tilka Manjhi Bhagalpur University
M.Sc. - Jawaharlal Nehru University
Ph.D. - Harish-Chandra Research Institute
Home page
B.Sc. and M.Sc. - National Taiwan University
Ph.D. - Columbia University
Home page