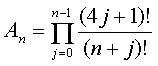Calculating the Limits of Poetic License:
Fictional Narrative and the History of Mathematics
Leo Corry - Tel Aviv University
| index | 1 | 2 | 4 |
4. Some Specific Examples:
What are the adequate limits of poetic license when it comes to mathematics in fiction? Are there, or should there be, any limits at all? Before answering these questions while considering some specific cases, I would like to answer these questions by considering, in some detail two successful pieces of mathematics in fiction: Apostolos Doxiadis' Uncle Petros and the Goldbach Conjecture and Ira Hauptman’s Partition.
(This picture is of the cover of the Hebrew version, one of the more than twenty languages to which it was translated.)
This is the story of an imaginary Greek mathematician, Petros Papachristos, as told by an admiring, if baffled, nephew who is also the unnamed narrator of the book. Throughout his life Petros has been obsessed by the drive to prove a number-theoretical conjecture first formulated in 1742 by Christian Goldbach, and that asserts that every even number bigger than 2 is the sum of two prime numbers. After completing his own training as a mathematician, the nephew becomes obsessed with finding out the true story of his uncle, whom other members of the family generally consider a failure.
The plot of the story is adequately set within a true historical framework, which definitely bestows its fictional parts with immediate credibility. Thus, for instance, the life of the fictional Uncle Petros is reliably embedded -- at both the personal and professional level -- in the Cambridge of Hardy, Littlewood and Ramanujan, where he studies in 1917-19.
There is, for example, a description of the analytic against the algebraic tradition in number theory and the status of the two at the beginning of the twentieth century, in order to provide the natural framework for Uncle Petros' own work. Partition-related results are mentioned in association with Ramanujan, whose death in 1920 comes at the right time from the point of view of Petros' quest to proving a result he was afraid Ramanujan would prove before him. Briefly said: there is a correct historical and mathematical setting of fiction inside reality, and the narrative tension of the plot is comfortably built on this correct basis. The reader of this book has every reason to suspend disbelief and let the author led him through the story.
One interesting detail of how the historical background is used relates to Petros' PhD studies in Berlin. The narrator tells us that Petros completed his dissertation in 1916 and that his advisor was Constantin Carathéodory, the foremost Greek mathematician of his generation, if not well-beyond it.
Thus, the already firm reliability of the story is further supported by the fact that a prominent Greek mathematician, who indeed was professor at the great Berlin school of mathematics, is the advisor of the fictional Petros. There could be no better choice in terms of coherence and internal logic of the story. Nevertheless, a factual problem arises here: Carathéodory arrived in Berlin only in 1918!
Does this deviation from strict historical truth matters in any possible sense? Most readers will not even be aware of this rather marginal detail, to begin with, and in any case, this could provide a classical example of poetic license taken by an author that no reader would bother protesting about. Not only it provides no sudden reason for giving up suspense of disbelief, but, as already said, it actually serves very well the plot and plays an actual role in helping put forward a coherently and convincing story. One might perhaps claim that the plot should have been conveniently modified on behalf of historical exactness in this case, but there is no real reason to complain about the poetic license taken by the author.
Let us look at a second, interesting place where the plot deviates from the historical record, while providing further support to the plot. In a dialogue between the narrator and his uncle Petros, reference is made to a famous lecture presented by David
Hilbert at the occasion of the 1900 Paris International Congress of Mathematicians.

This dialogue is meant to provide a glimpse into the way that absolute certainty was expected to pervade mathematics at the turn of the twentieth century, which was also the attitude that guided Petros in his own mathematical activities. Hilbert is presented as the champion of this view, as embodied in two famous sayings quoted by the narrator: "Wir müssen wissen, wir werden wissen" (we must know, we shall know), and "there is no ignorabimus in mathematics". Thus the narrator says: "Thus spake the great David Hilbert in the International Congress of 1900. A proclamation of mathematics as the Heaven of Absolute Truth. The vision of Euclid, the vision of Consistency and Completeness…"
Well, there are some problems in this description of what Hilbert said at that opportunity, and the most immediate one concerns the "Wir müssen wissen, wir werden wissen". These words, later engraved in Hilbert's tombstone,


were not part of the Paris address, but rather of a talk given in 1930 at a meeting in Königsberg to honour Hilbert on the occasion of being awarded the honorary citizenship of his native town.

Hilbert also broadcasted a speech in the local radio (which was recorded and later made available on a 45 record and recently digitalized). It is in that speech that his famous words appear, as the closing sentence that encapsulates Hilbert's legendary, unbridled feeling of scientific optimism. It is a remarkable coincidence that Hilbert gave this speech during a week in which four mathematical meetings were simultaneously held in Königsberg. In one of those meetings Kurt Gödel presented for the first time his first incompleteness theorem. The results developed by Gödel came to imply a serious blow to the program that Hilbert had been promoting for more than ten years now to prove the consistency of arithmetic by finitary methods. But neither in Königsberg in 1930 nor ever thereafter, Hilbert and Gödel met or listened to each other's talk.

"The story is so dramatic that it resembles fiction", has remarked Gregory Chaitin commenting this situation. In Königsberg while Hilbert was declaring "Wir müssen wissen, wir werden wissen", Gödel was speaking about inherent limitations in mathematical knowledge. We tend naturally to consider a situation of this kind more likely to be fiction than historical reality.
At any rate, what Hilbert did say in his 1900 speech was not very far away in spirit from what came to be engraved in his tombstone. He thus said:
This conviction of the solvability of any mathematical problem is a powerful incentive to the worker. We hear within us the perpetual call: There is the problem, seek its solution. You can find it by pure reason, for in mathematics there is no ignorabimus.
Interestingly, in terms of poetic license, it is uncle Petros himself who stresses the correct litmus test for the use of Hilbert's quotation in the context of a fictional story. "It is not the background", he says to his nephew, as he tries to explain how the import of Hilbert's putative assertion in the speech should be understood: "it’s the psychology. You have to understand the emotional climate in which mathematicians worked in those happy days , before Kurt Gödel”. Being a fictional character himself Uncle Petros is fully aware that what counts in this case is not to describe the things that has been, but rather what a man of Hilbert's "kind would probably or necessarily say" in such circumstances. It is the metaphorical Hilbert, not the historical one, who makes the 1900 speech in the book and the metaphorical Hilbert could by all means have added the sentence that was said only thirty years later. Curiously, however, the famous sentence has been repeated so frequently as having been said in 1900 that it has come to be considered as historically true. Many websites and serious books present it as a word-by-word quotation of what Hilbert said in 1900.
And yet, it is evident that an author of fiction like Doxiadis makes considerable efforts to keep his fiction within well-defined boundaries of historical accuracy and to allow himself poetic license only where truly necessary. The dramatic effect of his plot is achieved by a correct balance between the two aspects, fiction and historical reality. Thus, a close look at those places where fiction does override fact in his plot may be instructive about the triangle relationship under inspection here: mathematics, history, fictional narrative. These places are few, but they interestingly differ from each other.
The example of Carathéodory's years in Berlin is the easiest and less interesting. Here we have a clear historical fact (a date, a place, a name, a publication) incorrectly mentioned in the plot. As we saw in the example of Borges' story, mistakes likes this one may be incurred intentionally and with the aim in mind of strengthening the fictional effect. When unintended they may be caused either by simple oversight or by mistaken information. In the present example, it is so marginal that it can hardly affect either the reader's willingness to suspend disbelief or any other aspect of her engagement with the plot.
The case of Hilbert's quotation is much more interesting, and not because his words were said only thirty years after what the narrator attributes. The interesting point concerns the image of Hilbert presented here by the narrator and endorsed by Uncle Petros: "A proclamation of mathematics as the Heaven of Absolute Truth. The vision of Euclid, the vision of Consistency and Completeness." In this case we are talking about historical questions that are much subtler and elusive than the date of arrival of a mathematician in a certain city, or than the exact words he said in a speech. Historians of mathematics make their living by examining complex claims of this kind, and by trying to assess them critically against new evidence or against a fresh reading of well known texts. And indeed, recent historical research of mathematics at the turn of twentieth century, and in particular of the role of Hilbert within it, has led to conceive the description embodied in the above quotation as essentially erroneous, even if it was widely accepted as correct in the not too distant past.[*] The same historiographical point of view would imply a feeling of uneasiness with the claim that Gödel's work had the immediate effect of profoundly changing the way that mainstream mathematicians go about their research and would possibly abandon plans they were currently involved with (as is the case with Uncle Petros in the book). But if we follow Aristotle's distinction between history and poetry we should not be worried by this at all when assessing the value of any piece mathematics in fiction. We should only ask whether, while incurring in poetic license, the narrative is able to continue eliciting our willingness to suspend disbelief and carry on with the story, the plot and its characters.
In order to get at a third kind of possible way of fiction overriding fact, which in my opinion is by far the most interesting and challenging one for both the author and the reader of mathematics in fiction, I would like to draw attention to a short sentence added by Doxiadis to the book, outside the plot, thanking three mathematicians, Ken Ribet, Keith Conrad and Kevin Buzzard for carefully reading the revised manuscript and correcting "numerous mistakes”. On reading this statement, one wonders what kinds of mistakes would an author like Doxiadis want to make sure that he is avoiding in his text, and what kind of questions would he pose to his mathematical proofreaders in this regard. It is more than natural to expect that no one would like mathematical mistakes to enter a text of mathematics in fiction, and in general, I guess, such mistakes would be considered more damaging to the literary value of the text than unintended historical mistakes of a similar caliber.[*] Unintended historical mistakes are most unwelcome, of course, but they are never considered to be totally lethal for the book, and certainly not as lethal as a mathematical mistake would be. Moreover, in the final account historical inaccuracies may always pass as part of the poetic license that the author consciously undertook. But -- and this is the interesting point -- whereas we can conceive in mathematics in fiction (as in fiction in general) of intended departures from the historical record on behalf of the literary aims pursued by the author, I can hardly imagine a similar move involving a mathematical "fact".
Let us think, for instance, about an imaginary book called "Aunt Maria and the ASM Conjecture". The main character is the imagined Ecuadorian mathematician Maria Madre-de-Dios, who completed a PhD at MIT in 1980 under Gian Carlo Rota, and became obsessed with solving the Alternating Sign Matrix Conjecture. Her niece, who narrates the story, happens to be a historian of modern mathematics who is well aware of the most up-to-date conceptions held by the leading researchers in the field and of the most recondite, current debates in the profession. She is able to tell a story involving Sylverster, MacMahon, Schur, Mills, Robbins, Rumsey, Zeilberger, and all the rest, while ensuring that no high-brow scholar will be be able to point out this or that historical inaccuracy in her plot. Throughout the entire book, however, the ASM conjecture is described as follows:
Let An be the number of alternating sign matrices of dimension n×n bordered by +1s. Then
Moreover, let us assume that the story is so written that based on this formulation of the conjecture, the author is able to enhance the basis for the credibility of the narrative fiction underlying the plot; for instance, that this is the key to unlocking the mystery of a series of murders in an Ivy League mathematics department.[*] I would like to think of this imagined story as a possible blueprint for the ultimate mathematics in fiction, which, to the best of my knowledge is yet to be carried out. This is a kind of poetic license that I think to be less frequently found, if at all, and to offer a true challenge to be met. It would pose a subtle exercise in intellectual flexibility to prospective readers. It would certainly put to test the ability of recalcitrant mathematicians to suspend disbelief under the very adverse conditions implied by having to bear for long with a mistakenly rendered formula.
To be sure, anyone of us who knows some mathematics and/or some history of mathematics automatically becomes (to the effects of reacting to mathematics in fiction) a suspect recalcitrant mathematician or high-brow scholar. One will certainly find it hard to pass in silence the deliberate distortion of the historical or mathematical record as known to him or her, on behalf of any piece of good-quality mathematics in fiction, even after having read and apparently assimilated Aristotle's useful distinction. This distinction may help our intellect react with equanimity to poetic license taken by authors in such cases, but it will not always help our guts to the same extent. We can still be fully justified to fear that, at the bottom line, the public perception of science will be much more strongly shaped by mathematics in fiction (books and films) than by scholarly research on history of mathematics. This is equally valid for mathematics as it is for Amadeus and music, for Downfall and the public perception of Hitler and the end of World War II, for The Da Vinci Code and the history of religion and of art, and for Mel Gibson’s The Passion of Christ in its own relevant fields. And more examples could be added to this list. But of course, there is a big difference in the symbolic and emotional load associated with each of these topics and the amount of people to which they are directly relevant. In this sense the esoteric and essentially neutral character of mathematics and its basic estrangement from worldly affairs makes, generally speaking, the entire debate about mathematics and narrative fiction much more relaxed and detached than with any other topic.
The reader may find it instructive to consider now any other examples of his choice, in the light of the ideas presented here, and see if the latter are of any help in addressing the former. I have chosen to comment here, in concluding this section, on yet another work represented at the Myknons meeting, the play Partition, written by Ira Hauptman and originally set to stage by Barbara Oliver.
This play explores the relationship between Hardy and Ramanujan at Cambridge. While bound together by their deep love to mathematics and particularly to number theory, one could hardly think of two more different men, in terms of their cultural backgrounds, their religious convictions, their relationship to other human beings, and even their approach to mathematics. For Hardy the concept of rigorous proof embodied the essence of mathematics and therefore he tried, largely unsuccessfully, to teach it to Ramanujan. There are other three characters in the play: Billington, a fictional Trinity College classics professor and friend of Hardy, the goddess Namagiri (who was the personal deity of the real-life Ramanujan in India), and Pierre de Fermat.

In the play Namagiri interacts with Ramanujan in various aspects of his day-to-day life, and continually provides him with mathematical ideas and insights. In fact she literally writes with her finger some of Ramanujan's fascinating equations on his tongue. Namagiri also consults Fermat on the possible way to solve FLT, and at some point Fermat confesses that he does not remember the original proof of his theorem, written many years ago in the narrow margins of his copy of Diophantus' book. Based on a hint by Namagiri, Ramanujan suggests Hardy a possible way to solve FLT which is close to the way in which Andrew Wiles proved in 1993 the Taniyama-Shimura Conjecture from which the validity of FLT derives.
It is well known to mathematicians that Hardy and Ramanujan never worked on FLT. One may guess that, if while watching Partition some mathematicians start moving uncomfortably on their seats, this will be caused directly, in most cases, by this deviation from the known historical record concerning mathematical facts. Most mathematicians will find it more easy to accept that a Hindu goddess speaks (in English) with a seventeenth-century mathematician about a recondite problem and that then she transmits (in English) the knowledge acquired to Ramanujan. It is remarkable that in a review of the play published for the Notices of the AMS by the Berkeley number-theorist Ken Ribet he addressed this point and he solved the tension that the play created in this mind, by referring to terms very close in spirit to what I have suggested above. This is what he wrote:
Professional mathematicians who saw the play were disturbed by the prominent roles given to Fermat and his Last Theorem, since the real Ramanujan and Hardy did no work on this particular problem. I personally was startled by the implicit anachronistic suggestion that Ramanujan was close to finding a proof of Fermat’s Last Theorem that relied on Galois representations, modular forms, Euler systems, and Selmer groups.
In order to enjoy the play, one must relax the implicit identification between the historical Hardy–Ramanujan and the characters on stage. Theater-goers who have little problem observing a goddess in discussion with a seventeenth-century mathematician on stage can make their peace with a historical distortion that allows the audience to hook up with a familiar and famous problem. Once I was able to separate the real Hardy and Ramanujan from their counterparts on stage, I found only good things to say about “Partition”.
Although at first reticent to accept the mathematical anachronism implied in the plot, Ribet can nevertheless come to terms with it by implicitly adopting the Aristotelian distinction about the plot and characters featured in the play. But I wonder how this willingness to accept poetic license would work if the play contained an inaccuracy pertaining, not the history of the subject, but rather some part in its core body of knowledge (such as the formulation of a result or the details of a certain proof). Unfortunately, this is not a question that can be easily answered for lack of significant, relevant examples.
Hauptman’s choice of FLT as the mathematical focus of her play seems rather natural and is hardly surprising. Indeed, given the enormous public attention that FLT attracted in the wake of Wiles’ proof (and about which more is said in the next section) it became a favorite of writers of mathematics in fiction. Indeed, one of the most ingenious examples of poetic license that I can mention here is related to FLT and appears in a rather unlikely setting: the TV cartoon series The Simpsons. This is a mathematical joke that appears in a broader context, rather than a real work of mathematics in fiction. And yet it touches upon the core point of what might be the real test for poetic license in mathematics in fiction. Although very minor in scope, this example concerns the body of a well-known mathematical result and distorts it in a rather cavalier and unapologetic way. As is well known, FLT establishes that for n > 2, the equation
xn + yn = zn
has no non-trivial, integer solution. Two “counterexamples” to FLT appear in episodes of the series. The first, 178212 + 184112 = 192212, is correct up to 9 decimal digits, whereas the second 398712 + 436512 = 447212 is correct up to 10 decimal digits. In other words, the mathematical fact has not only been distorted, but it has been in a way that is not immediately detectable. Indeed, because of rounding-off errors, these equations will appear as correct in most handheld calculators.[*]
In the next section I would like to consider the triangular relationship from a different perspective, namely, how the dramatic dimension enters the writing of historical accounts of mathematics, mainly of the popular kind.
| index | 1 | 2 | 4 |