
Discussion of the Question 07/03
HULA HOOP
The question was:

What movement should be performed by a person rotating a hoop round his body?
(9/03) Y. Kantor:
We got quite a large amount of emails considering the kinematics in
its simplest form. Since we are dealing with quite a complicated system,
let us split the "general" question into a sequence of simpler questions.
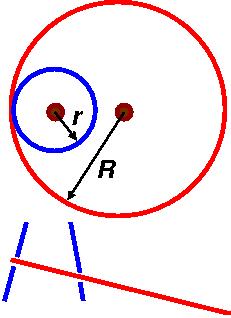
Stage A: Assume that the body has circular cross-section. Its radius
r may depend on height. The hoop has radius R. See the
following picture, depicting top and side views (top and bottom of the
picture). If we completely disregard energy losses, there is no need to move
the body, and the center of mass
of the hoop will perform a circular motion around the center of the body
and the radius of that motion will be Rcos(a)-r,
where a is the angle between the plane of the hoop and a horizontal
plane.
In the idealized situation described above, what will be the force
between the body and the hoop? How the frequency of the rotation of the
hoop is related to parameters of the problem (including "body shape", i.e.
dependence of r on height)? Is there an optimal frequency? What is
the angle a?
Stage B: How will the above answers change if the body does not have a circular
cross section. (Consider a case of ellipse.)
Stage C: In the presence of losses, what kind of motion should be performed
to "inject" energy into the hoop.
(6/05) Y. Kantor: In March 2004 issue of
Biological Cybernetics was published a paper
entitled "Coordination Modes in the Multi-Segmental Dynamics of Hula-Hooping"
(see it in the pdf format). It was
later awarded the jokular Ig Nobel award. Some interesting data on
hula-hooping can be found there.
 Back to "front page"
Back to "front page"



 Back to "front page"
Back to "front page"