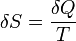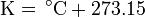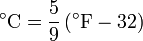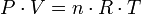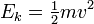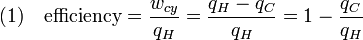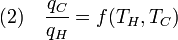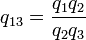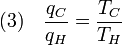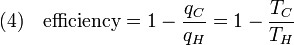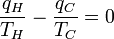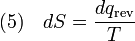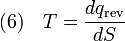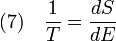Temperature
In thermodynamics, temperature is a measure of the tendency of an object or system to spontaneously give up energy. Temperature is a physical property of a system that underlies the common notions of "hot" and "cold", in which something that is hotter has the greater temperature. Temperature arises from the random microscopic motions of matter, where temperature is related to the average kinetic energy of these microscopic motions. The concept of temperature, defined as a tension associated with entropy, follows from the zeroth law of thermodynamics.
Temperature is measured with thermometers that may be calibrated to a variety of temperature scales. Throughout the world (except for the U.S.), the Celsius scale is used for most temperature measuring purposes. The entire scientific world (the U.S. included) measures temperature in Kelvins on the thermodynamic (absolute) temperature scale and in Celsius. Many engineering fields in the U.S., especially high-tech ones, also use the Kelvin and Celsius scales. The bulk of the U.S. however, (its lay people, industry, meteorology, and government) relies upon the Fahrenheit scale. Other engineering fields in the U.S. also rely upon the Rankine scale when working in thermodynamic-related disciplines such as combustion. The different temperature scales can be transformed into each other by means of temperature conversion, for which conversion tables and automated tools are available.
Contents |
[edit] Overview
Temperature is a measure of the average energy contained in the microscopic degrees of freedom of a system. For example, in an ideal gas, the relevant degrees of freedom are translational, rotational, and vibrational motion of the individual molecules. In this case, temperature is proportional to the mean kinetic energy of the constituent atoms. But in more complicated systems, magnetic, electronic, photonic, or other exotic degrees of freedom can play a significant role in determining temperature.
Thermal motion is the reason gasses have pressure, since the particles in the gas collide with the walls of the container and exert an outward force. Although very specialized laboratory equipment is required to directly detect thermal motions, thermal collisions by atoms or molecules with small particles suspended in a fluid produces Brownian motion that can be seen with an ordinary microscope. The thermal motions of atoms are very fast and temperatures close to absolute zero are required to directly observe them. For instance, when scientists at the NIST achieved a record-setting cold temperature of 700 nK (billionths of a kelvin) in 1994, they used optical lattice laser equipment to adiabatically cool caesium atoms. They then turned off the entrapment lasers and directly measured atom velocities of 7 mm per second in order to calculate their temperature.
Molecules, such as O2, have more degrees of freedom than single atoms: they can have rotational and vibrational motions as well as translational motion. An increase in temperature will cause the average translational energy to increase. It will also cause the energy associated with vibrational and rotational modes to increase. Thus a diatomic gas, with extra degrees of freedom like rotation and vibration, will require a higher energy input to change the temperature by a certain amount, i.e. it will have a higher heat capacity than a monatomic gas.
The process of cooling involves removing energy from a system. When there is no more energy able to be removed, the system is said to be at absolute zero, which is the point on the thermodynamic (absolute) temperature scale where all kinetic motion in the particles comprising matter ceases and they are at complete rest in the “classic” (non-quantum mechanical) sense. By definition, absolute zero is a temperature of precisely 0 kelvins (–273.15 °C or –459.67 °F).
[edit] Details
The formal properties of temperature are studied in thermodynamics and statistical mechanics. The temperature of a system at thermodynamic equilibrium is defined by a relation between the amount of heat δQ incident on the system during an infinitesimal quasistatic transformation, and the variation δS of its entropy during this transformation.
Contrary to entropy and heat, whose microscopic definitions are valid even far away from thermodynamic equilibrium, temperature can only be defined at thermodynamic equilibrium, or local thermodynamic equilibrium (see below).
As a system receives heat its temperature rises, similarly a loss of heat from the system tends to decrease its temperature (at the - uncommon - exception of negative temperature, see below).
When two systems are at the same temperature, no heat transfer occurs between them. When a temperature difference does exist, heat will tend to move from the higher-temperature system to the lower-temperature system, until they are at thermal equilibrium. This heat transfer may occur via conduction, convection or radiation (see heat for additional discussion of the various mechanisms of heat transfer).
Temperature is also related to the amount of internal energy and enthalpy of a system. The higher the temperature of a system, the higher its internal energy and enthalpy are.
Temperature is an intensive property of a system, meaning that it does not depend on the system size or the amount of material in the system. Other intensive properties include pressure and density. By contrast, mass and volume are extensive properties, and depend on the amount of material in the system.
[edit] The role of temperature in nature
Temperature plays an important role in almost all fields of science, including physics, chemistry, and biology.
Many physical properties of materials including the phase (Solid, liquid, gaseous or plasma), density, solubility, vapor pressure, and electrical conductivity depend on the temperature. Temperature also plays an important role in determining the rate and extent to which chemical reactions occur. This is one reason why the human body has several elaborate mechanisms for maintaining the temperature at 37 °C, since temperatures only a few degrees higher can result in harmful reactions with serious consequences. Temperature also controls the type and quantity of thermal radiation emitted from a surface. One application of this effect is the incandescent light bulb, in which a tungsten filament is electrically heated to a temperature at which significant quantities of visible light are emitted.
Temperature-dependence of the speed of sound in air c, density of air ρ and acoustic impedance Z vs. temperature °C
| Impact of temperature on speed of sound, air density and acoustic impedance | |||
| T in °C | c in m/s | ρ in kg/m³ | Z in N·s/m³ |
| −10 | 325.4 | 1.341 | 436.5 |
| −5 | 328.5 | 1.316 | 432.4 |
| 0 | 331.5 | 1.293 | 428.3 |
| 5 | 334.5 | 1.269 | 424.5 |
| 10 | 337.5 | 1.247 | 420.7 |
| 15 | 340.5 | 1.225 | 417.0 |
| 20 | 343.4 | 1.204 | 413.5 |
| 25 | 346.3 | 1.184 | 410.0 |
| 30 | 349.2 | 1.164 | 406.6 |
[edit] Temperature measurement
Main article: Temperature measurement, see also The International Temperature Scale.
Temperature measurement using modern scientific thermometers and temperature scales goes back at least as far as the early 18th century, when Gabriel Fahrenheit adapted a thermometer (switching to mercury) and a scale both developed by Ole Christensen Rømer. Fahrenheit's scale is still in use, alongside the Celsius scale and the Kelvin scale.
[edit] Units of temperature
The basic unit of temperature (symbol: T) in the International System of Units (SI) is the kelvin (K). One kelvin is formally defined as exactly 1/273.16 of the temperature of the triple point of water (the point at which water, ice and water vapor exist in equilibrium). This puts the freezing point of water (which cannot be measured with high precision) and the zero point of the Celsius scale at 273.15, not 273.16. The (unattainable) temperature 0 K is called absolute zero and corresponds to the point at which the molecules and atoms have the least possible thermal energy. An important unit of temperature in theoretical physics is the Planck temperature (1.4 × 1032 K).
In the field of plasma physics, because of the high temperatures encountered and the electromagnetic nature of the phenomena involved, it is customary to express temperature in electronvolts (eV) or kiloelectronvolts (keV), where 1 eV = 11,605 K. In the study of QCD matter one routinely meets temperatures of the order of a few hundred MeV, equivalent to about 1012 K.
For everyday applications, it is often convenient to use the Celsius scale, in which 0 °C corresponds to the temperature at which water freezes and 100 °C corresponds to the boiling point of water at sea level. In this scale a temperature difference of 1 degree is the same as a 1 K temperature difference, so the scale is essentially the same as the Kelvin scale, but offset by the temperature at which water freezes (273.15 K). Thus the following equation can be used to convert from degrees Celsius to kelvins.
In the United States, the Fahrenheit scale is widely used. On this scale the freezing point of water corresponds to 32 °F and the boiling point to 212 °F. The following formula can be used to convert from Fahrenheit to Celsius:
See temperature conversion formulas for conversions between most temperature scales.
[edit] Negative temperatures
- See main article: Negative temperature.
For some systems and specific definitions of temperature, it is possible to obtain a negative temperature. A system with a negative temperature is not colder than absolute zero, but rather it is, in a sense, hotter than infinite temperature.
[edit] Theoretical foundation of temperature
[edit] Zeroth-law definition of temperature
While most people have a basic understanding of the concept of temperature, its formal definition is rather complicated. Before jumping to a formal definition, let us consider the concept of thermal equilibrium. If two closed systems with fixed volumes are brought together, so that they are in thermal contact, changes may take place in the properties of both systems. These changes are due to the transfer of heat between the systems. When a state is reached in which no further changes occur, the systems are in thermal equilibrium.
Now a basis for the definition of temperature can be obtained from the so-called zeroth law of thermodynamics which states that if two systems, A and B, are in thermal equilibrium and a third system C is in thermal equilibrium with system A then systems B and C will also be in thermal equilibrium (being in thermal equilibrium is a transitive relation; moreover, it is an equivalence relation). This is an empirical fact, based on observation rather than theory. Since A, B, and C are all in thermal equilibrium, it is reasonable to say each of these systems shares a common value of some property. We call this property temperature.
Generally, it is not convenient to place any two arbitrary systems in thermal contact to see if they are in thermal equilibrium and thus have the same temperature. Also, it would only provide an ordinal scale.
Therefore, it is useful to establish a temperature scale based on the properties of some reference system. Then, a measuring device can be calibrated based on the properties of the reference system and used to measure the temperature of other systems. One such reference system is a fixed quantity of gas. The ideal gas law indicates that the product of the pressure and volume (P · V) of a gas is directly proportional to the temperature:
where T is temperature, n is the number of moles of gas and R is the universal gas constant. Thus, one can define a scale for temperature based on the corresponding pressure and volume of the gas: the temperature in kelvins is the pressure in pascals of one mole of gas in a container of one cubic metre, divided by 8.3144 (the value of R in the pertinent units). In practice, such a gas thermometer is not very convenient, but other measuring instruments can be calibrated to this scale.
The ideal gas law equation indicates that for a fixed volume of gas, the pressure increases with increasing temperature. Pressure is just a measure of the force applied by the gas on the walls of the container and is related to the energy of the system. Thus, we can see that an increase in temperature corresponds to an increase in the thermal energy of the system. When two systems of differing temperature are placed in thermal contact, the temperature of the hotter system decreases, indicating that heat is leaving that system, while the cooler system is gaining heat and increasing in temperature. Thus heat always moves from a region of high temperature to a region of lower temperature and it is the temperature difference that drives the heat transfer between the two systems.
[edit] Temperature in gases
For a monatomic ideal gas the temperature is related to the translational motion or average speed of the atoms. The kinetic theory of gases uses statistical mechanics to relate this motion to the average kinetic energy of atoms and molecules in the system. This average energy is independent of particle mass, which seems counterintuitive to many people. Although the temperature is related to the average kinetic energy of the particles in a gas, each particle has its own energy which may or may not correspond to the average. However, after an examination of some basic physics equations it makes perfect sense. The second law of thermodynamics states that any two given systems when interacting with each other will later reach the same average energy. Temperature is a measure related to the average kinetic energy of a system. The formula for the kinetic energy of an atom is:
(Note that a calculation of the kinetic energy of a more complicated object, such as a molecule, is slightly more involved. Additional degrees of freedom are available, so molecular rotation or vibration must be included.)
Thus, particles of greater mass (say a neon atom relative to a hydrogen molecule) will move slower than lighter counterparts, but will have the same average energy. This average energy is independent of the mass because of the nature of a gas, all particles are in random motion with collisions with other gas molecules, solid objects that may be in the area and the container itself (if there is one). A visual illustration of this from Oklahoma State University makes the point more clear. Particles with different mass have different velocity distributions, but the average kinetic energy is the same because of the ideal gas law. In a gas the distribution of energy (and thus speeds) of the particles corresponds to the Boltzmann distribution.
[edit] Temperature of the vacuum
The temperature of an object is proportional to the average kinetic energy of the molecules in it. In a pure vacuum, there are no molecules. There is nothing to measure the kinetic energy of, and temperature is undefined. If a thermometer were placed in a vacuum, the reading would be a measurement of the internal temperature of the thermometer, not of the vacuum which surrounds it.
All objects emit black body radiation. Over time, a thermometer in a pure vacuum will radiate away thermal energy, decreasing in temperature indefinitely until it reaches the zero-point energy limit.
In practice, there is no such thing as a pure vacuum since there will always be photons associated with the black body radiation of the walls of the vacuum. A thermometer orbiting the Earth can easily absorb energy from sunlight faster than it can radiate it away. This can lead to a dramatic temperature increase.
A thermometer isolated from solar radiation (in the shade of a larger body, for example) is still exposed to Cosmic microwave background radiation. In this case, the temperature will change until the rate of energy loss and gain are in equilibrium. At this point, the thermometer will have a temperature of 2.725 K, which is often referred to as the temperature of space.
[edit] Second-law definition of temperature
In the previous section temperature was defined in terms of the Zeroth Law of thermodynamics. It is also possible to define temperature in terms of the second law of thermodynamics, which deals with entropy. Entropy is a measure of the disorder in a system. The second law states that any process will result in either no change or a net increase in the entropy of the universe. This can be understood in terms of probability. Consider a series of coin tosses. A perfectly ordered system would be one in which every coin toss would come up either heads or tails. For any number of coin tosses, there is only one combination of outcomes corresponding to this situation. On the other hand, there are multiple combinations that can result in disordered or mixed systems, where some fraction are heads and the rest tails. As the number of coin tosses increases, the number of combinations corresponding to imperfectly ordered systems increases. For a very large number of coin tosses, the number of combinations corresponding to ~50% heads and ~50% tails dominates and obtaining an outcome significantly different from 50/50 becomes extremely unlikely. Thus the system naturally progresses to a state of maximum disorder or entropy.
We previously stated that temperature controls the flow of heat between two systems and we have just shown that the universe, and we would expect any natural system, tends to progress so as to maximize entropy. Thus, we would expect there to be some relationship between temperature and entropy. In order to find this relationship let's first consider the relationship between heat, work and temperature. A heat engine is a device for converting heat into mechanical work and analysis of the Carnot heat engine provides the necessary relationships we seek. The work from a heat engine corresponds to the difference between the heat put into the system at the high temperature, qH and the heat ejected at the low temperature, qC. The efficiency is the work divided by the heat put into the system or:
where wcy is the work done per cycle. We see that the efficiency depends only on qC/qH. Because qC and qH correspond to heat transfer at the temperatures TC and TH, respectively, qC/qH should be some function of these temperatures:
Carnot's theorem states that all reversible engines operating between the same heat reservoirs are equally efficient. Thus, a heat engine operating between T1 and T3 must have the same efficiency as one consisting of two cycles, one between T1 and T2, and the second between T2 and T3. This can only be the case if:
which implies:
- q13 = f(T1,T3) = f(T1,T2)f(T2,T3)
Since the first function is independent of T2, this temperature must cancel on the right side, meaning f(T1,T3) is of the form g(T1)/g(T3) (i.e. f(T1,T3) = f(T1,T2)f(T2,T3) = g(T1)/g(T2)· g(T2)/g(T3) = g(T1)/g(T3)), where g is a function of a single temperature. We can now choose a temperature scale with the property that:
Substituting Equation 3 back into Equation 1 gives a relationship for the efficiency in terms of temperature:
Notice that for TC = 0 K the efficiency is 100% and that efficiency becomes greater than 100% below 0 K. Since an efficiency greater than 100% violates the first law of thermodynamics, this implies that 0 K is the minimum possible temperature. In fact the lowest temperature ever obtained in a macroscopic system was 20 nK, which was achieved in 1995 at NIST. Subtracting the right hand side of Equation 5 from the middle portion and rearranging gives:
where the negative sign indicates heat ejected from the system. This relationship suggests the existence of a state function, S, defined by:
where the subscript indicates a reversible process. The change of this state function around any cycle is zero, as is necessary for any state function. This function corresponds to the entropy of the system, which we described previously. We can rearrange Equation 5 to get a new definition for temperature in terms of entropy and heat:
For a system, where entropy S may be a function S(E) of its energy E, the temperature T is given by:
Equation 7 states that the reciprocal of the temperature is the rate of increase of entropy with energy.
[edit] References
- Kroemer, Herbert; Kittel, Charles (1980). Thermal Physics (2nd ed.). W. H. Freeman Company. ISBN 0-7167-1088-9.
| |
Some content on this page may previously have appeared on Citizendium. |