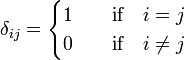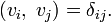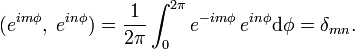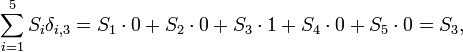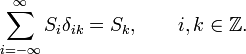Kronecker delta

From Knowino
Jump to: navigation, search

In mathematics, the Kronecker delta is a symbol, written as δij, depending on two integral numbers i and j. The symbol designates the number 1 if i = j and 0 if i ≠ j:

\delta_{ij} = \begin{cases} 1 &\quad\hbox{if}\quad i = j \\ 0 &\quad\hbox{if}\quad i \ne j \\ \end{cases}

The symbol is named after the German mathematician Leopold Kronecker (1823-1891).

The general element of an identity matrix can be written as a Kronecker delta: the diagonal elements (i = j) are one; the off-diagonal elements (i ≠ j) are zero.

In linear algebra and functional analysis the Kronecker delta appears to indicate orthonormality of certain sets of vectors (elements of a vector space). Indicating an inner product by brackets, two vectors are mutually orthogonal and individually normalized to unity if

(v_i,\; v_j) = \delta_{ij}.

An example may be taken from Fourier analysis:

(e^{im\phi},\; e^{in\phi}) = \frac{1}{2\pi} \int_{0}^{2\pi} e^{-im\phi}\, e^{in\phi} \mathrm{d}\phi = \delta_{mn}.

Kronecker deltas appear frequently in summations where they act as a "filter". To clarify this we consider a simple example

\sum_{i=1}^5 S_i \delta_{i,3} = S_1 \sdot0 + S_2 \sdot0 +S_3 \sdot1 +S_4 \sdot0 +S_5 \sdot0 = S_3,

that is, the element S3 is "filtered out" of the summation by δi,3.

In general, (i and k integers)

\sum_{i=-\infty}^{\infty} S_{i}\delta_{ik} = S_k,\qquad i,k \in \mathbb{Z}.

See Dirac delta function for a generalization of the Kronecker delta to real i and j.

Retrieved from "http://knowino.org/wiki/Kronecker_delta"
Personal tools
Variants
Actions
Navigation
Community
Toolbox