Internal energy
In thermodynamics, a system is any object, any quantity of matter, any region, etc. selected for study and mentally set apart from everything else which is then called its surroundings. The imaginary envelope enclosing the system and separating it from its surroundings is called the boundary of the system.[1] In this article the boundaries will be referred to as the walls of the system.
The internal energy of a system is simply its energy. The term was introduced into thermodynamics in 1852 by W. Thomson (the later Lord Kelvin).[2] The adjective "internal" refers to the fact that some energy contributions are not considered. For instance, when the total system is in uniform motion, it has kinetic energy. This overall kinetic energy is never seen as part of the internal energy; one could call it external energy. Or, if the system is at constant non-zero height above the surface the Earth, it has constant potential energy in the gravitational field of the Earth. Gravitational energy is only taken into account when it plays a role in the phenomenon of interest, for instance in a colloidal suspension, where the gravitation influences the up- downward motion of the small particles comprising the colloid. In all other cases, gravitational energy is assumed not to contribute to the internal energy; one may call it again external energy.
On the other hand, a contribution to internal energy that is always included is the kinetic energy of the atoms or molecules constituting the system. In an atomic gas, it is the energy associated with translations of the atoms; in a molecular gas translations and molecular rotations contribute to internal energy. In a solid, internal energy acquires contributions from vibrations, among other effects. Except for ideal gases, the potential energy of molecules in the field of the others (see intermolecular forces) is also an important component of the internal energy.
In general, energies that are not changing in the processes of interest are left out of the definition of internal energy. For instance, when a system consists of a vessel filled with water and the process of interest is evaporation (formation of steam), the kinetic energy of the water molecules and the interaction between them are included in the internal energy. As long as no chemical bonds are broken, the energies contained in these bonds are not included. If the temperatures are not too high, say below 200 to 300 °C, the intramolecular vibrational energies are ignored as well. Chemists and engineers never include relativistic contributions, of the type E = mc2, or nuclear contributions (say the fusion energy of protons with oxygen-nuclei). However, a plasma physicist studying the thermodynamics of fusion reactions will include nuclear energy in the internal energy of the plasma.
Contents |
[edit] First law of thermodynamics
Classical (phenomenological) thermodynamics is not concerned with the nature of the internal energy, it simply postulates that it exists and may be changed by certain processes. Further it is postulated that internal energy, usually denoted by either U or E, is a state function, that is, its value depends upon the state of the system and not upon the nature or history of the past processes by which the system attained its state. In addition, the internal energy, which henceforth will be written as U, is assumed to be a differentiable function of the independent variables that uniquely specify the state of the system. An example of such a state variable is the volume V of the system.
When the system has thermally conducting walls, an amount of heat DQ can go through the wall in either direction: if DQ > 0, heat enters the system and if DQ < 0 the system loses heat to its surroundings. The symbol DQ indicates simply a small amount of heat, and not a differential of Q. Note that, because it is not a function, Q does not have a differential. The internal energy of the system changes by dU as a consequence of the heat flow, and it is postulated that
Reiterating, the usual sign convention is such that positive DQ is the heat absorbed by the system, i.e., the heat that the system receives from its surroundings. The symbol dU indicates a differential of the differentiable function U.
Most thermodynamic systems are such that work can be performed on them or by them. When a small amount of work DW is performed by the system, the internal energy decreases,
The sign convention is such that DW is the work by the system on its surroundings, hence the minus sign in this equation.
As an example of work, consider a cylinder of volume V that may be changed by moving a piston in or out. The cylinder contains gas of pressure p. A small amount of work pdV is performed on the system by reversibly (quasi-statically) moving the piston inward (dV < 0). The sign convention of DW is such that DW and dV have the same sign
Due to the fact that the work is performed reversibly, the small amount of work DW is proportional to the differential dV. If dV > 0 (expansion), work DW > 0 is performed by the system. Hence the change in internal energy obtains indeed a minus sign:
Note that other forms of work than pdV are possible. For instance, DW = −HdM, the product of an external magnetic field H with a small change in total magnetization dM, is a change in internal energy caused by an alignment of the microscopic magnetic moments that constitute a magnetizable material.
An important form of doing work is the reversible addition of substance,
here μ (a function of thermodynamic parameters as T, p, etc.) is the chemical potential of the pure substance added to the system. The infinitesimal quantity dn is the amount (expressed in moles) of substance added. The chemical potential μ is the amount of energy that the system gains when reversibly, adiabatically (DQ = 0), and isochorically (dV = 0) a mole of substance is added to it.
When a small amount of heat DQ flows in or out the system and simultaneously a small amount of work DW is done by or on the system, the first law of thermodynamics states that the internal energy changes as follows
Note that the sum of two small quantities, both not necessarily differentials, gives a differential of the state function U. The first law, equation (1), postulates the existence of a state function that accumulates the work done on/by the system and the heat that flows in/out the system.
Internal energy is an extensive property—that is, its magnitude depends on the amount of substance in a given state. Often one considers the molar energy, energy per amount of substance (amount expressed in moles); this is an intensive property. Also the specific energy (energy per kilogram) is an intensive property. The (extensive) internal energy has the SI dimension joule.
Note that thus far only a change in internal energy was defined. An absolute value can be obtained by defining a zero (reference) point with U0 = 0 and integration
Since U is a state function U1 is independent of the integration path (the choice of values of S, V, and n between lower and upper bound of the integration). The reference point U0 could be at the zero of absolute temperature (zero kelvin).
[edit] Explicit expression
Consider a one-component thermodynamical system that allows heat exchange DQ, work −pdV, and matter exchange μdn. The second law of thermodynamics states that there exists a variable, entropy (commonly denoted by S) that is given by
that is, the integrating factor 1/T converts the small quantity DQ into the differential dS. This relation holds when the heat exchange occurs reversibly. By the second law, the entropy S is a state variable. It is size-extensive, i.e., S is linear in the size of the system, and has dimension J/K (joule per degree kelvin).
Since there are three forms of energy contact with the surroundings, the system has exactly three independent state variables. Choose now as independent set the variables S, V, and n, which all three are size-extensive. By results shown earlier, cf. equation (1), and use of DQ = TdS, the differential of the internal energy is
It will be shown that an explicit expression for the internal energy U of the system under consideration is,
In order to prove (3), we consider first two identical systems with the same values for the three size-extensive independent variables S, V, n (and hence also the same values for U, T, and p). Clearly, the "supersystem" consisting of the two identical system has twice the entropy, volume, and amount of substance, and the sum of the energies of the two systems is 2U, or
The same kind of equation holds when we separate the original system into two equal parts, then the energy, entropy, volume and amount of substance are halved for each of the two parts. Clearly then, for an arbitrary real positive number λ,
That is, the internal energy U is a homogeneous function of order 1 of the size-extensive variables, S, V and n. By Euler's theorem,
Since U is a function of the three variables, dU can be written in terms of partial derivatives. When this is equated to the expression in equation (2)
it follows (since S, V, and n are independent) that
Insertion of this into equation (4) gives the result (3).
[edit] Gibbs free energy
At first sight it may look as if equations (2) and (3) are contradictory, for, when taking the differential dU of (3), the term SdT −Vdp + ndμ arises, which is absent in equation (2). From the consistency of equations (2) and (3) it follows that SdT − Vdp + ndμ = 0. It is now shown that the latter expression yields an equation for the differential dG of the Gibbs free energy G.
The Gibbs free energy, often denoted by G in honor of the American physicist J. Willard Gibbs, is defined by
From equation (3) it follows immediately that G = μn and taking the differential gives dG = d(μn).
One can confirm that G = μn by means of differential expressions. From the definition of G:
Using
it follows that
Integration gives G = nμ + G0. Taking that the zero of Gibbs energy G0 = 0, it is confirmed that the chemical potential μ is the Gibbs free energy per mole, μ = G/n.
[edit] Statistical thermodynamics definition
Consider a system of constant temperature T, constant number of molecules N, and constant volume V. In statistical thermodynamics one defines for such a system the density operator
where Ĥ is the Hamiltonian (energy operator) of the total system, Tr(Ô) is the trace of the operator Ô, β = 1/(kT), and k is Boltzmann's constant. The quantity Q is the partition function.
The thermodynamic average of Ĥ is equal to the internal energy U,
The internal energy is minus the logarithmic derivative of Q,
Further
Hence, the following well-known statistical-thermodynamics expression is obtained for the internal energy U,
[edit] Notes
- The existence of an energy operator Ĥ was simply assumed. The choice of energy terms to be included in this operator, is in fact equivalent to the choice of contributions adding to the internal energy U. Statistical thermodynamics does not solve the problem of defining internal energy.
- When the trace is evaluated in a basis of eigenstates of Ĥ, the physical meaning of the density operator becomes clearer. In fact, Boltzmann weight factors will arise. Thus, upon writing,
- the partition function becomes [β = 1 /(kT)]:
- and the thermodynamic average becomes in a basis of energy eigenstates
- The partition function normalizes the Boltzmann weights, exp[− Ei/(kT)]. Indeed,
- The sum over normalized weights equals unity, as a proper weight function should.
[edit] Reference
- ↑ Perry's Handbook for Chemical Engineers, R. H. Perry and D. W. Green (editors), McGraw-Hill Companies, 6th ed. (1984) ISBN-10: 0070494797; ISBN-13: 978-0070494794
- ↑ W. Thomson, On a Universal Tendency in Nature to the Dissipation of Mechanical Energy, The Proceedings of the Royal Society of Edinburgh for April 19, 1852. Scanned copy of Kelvin's collected works


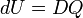
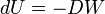
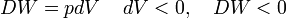
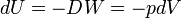
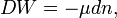
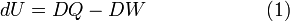
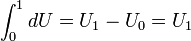
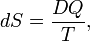


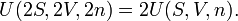
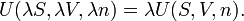
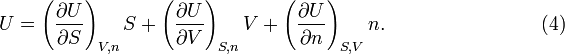
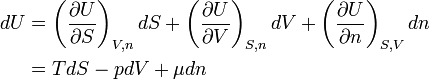
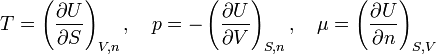
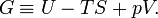
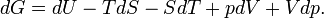
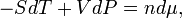
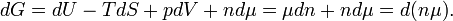
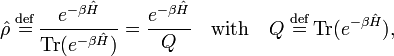
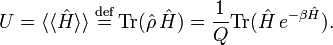
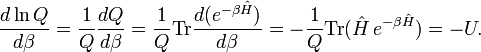
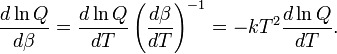
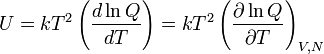
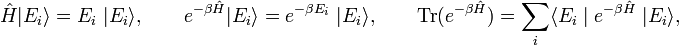
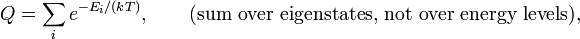
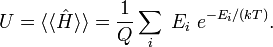
![\mathrm{Tr}(\hat{\rho}) = \frac{1}{Q}\left[ \sum_i e^{- E_i/(kT)} \right ] = \frac{Q}{Q} = 1.](../w/images/math/c/c/b/ccbaad24c692f403909d74b7e0cee2b5.png)