Answer to the Question 01/00
CLIMBING AN ICEBERGThe question was:
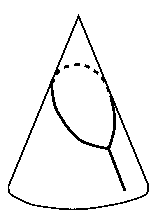
A mountaineer climbs an iceberg - icy cone-shaped mountain. He has made a loop with non-sliding knot and thrown it over the top of the mountain as shown in the figure. If the mountain is steep enough, the climber will reach the summit; if it is not, the loop will slip of the top. Find the critical slope of the mountain.
The problem has been solved (18/1/2000) by Jhinhwan Lee a Ph.D. student at Center for Science in Nanometer Scale at Seoul National University, Korea (e-mail jhinhwan@csns.snu.ac.kr), by Sumit Banerjee (13/2/2000) from Indian Institutes of Science and Astrophysics (e-mail sumit@iiap.ernet.in), and (26/2/2000) by Andrew Wiggin (e-mail awiggin@hotmail.com).
D. Khmelnitskii told us both the problem and its solution which is presented below. (See also the p.p.s. at the end!)
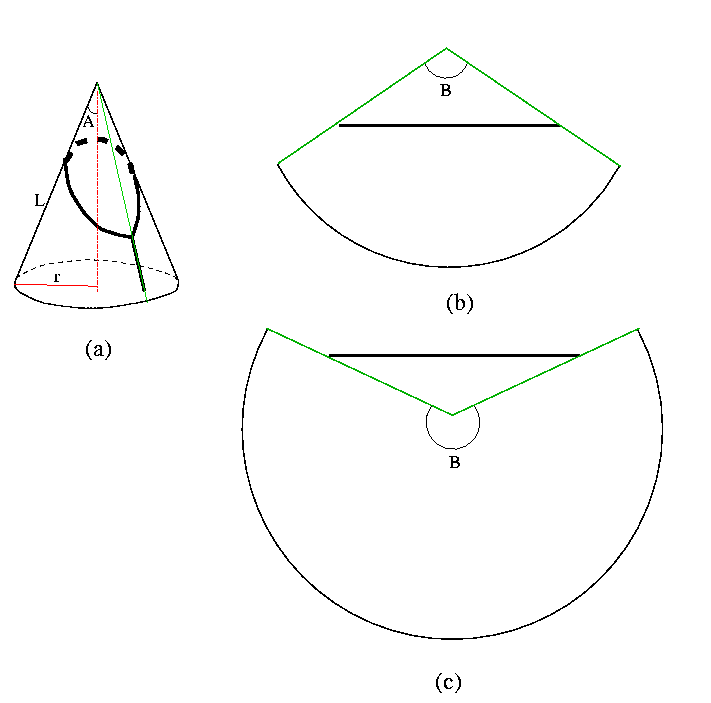
The answer: The critical angle A between the generatrix of the cone and the vertical (see Fig.(a) below) is 30o.
The solution:
The solution is given by a simple lemma, consisting in the following: Consider a rope on a convex surface with two equal weights at its ends. It is obvious that the length must be the shortest possible, otherwise the potential energy of the weights would not be minimum. So, according to the lemma, a rope on a convex surface lies along a geodesic line, i.e. the shortest curve between two points lying wholly on the surface.
Now, if we cut our cone along the generatrix, passing through the knot of the loop (green line on Fig.(a) below), and then roll it out on the plane, we will get a sector, which will look either like Fig.(b) or Fig.(c) below depending on the angle A. Green lines on the resulting sectors are just the line along which the cone was cut. Here the thick lines are the projections of the loop on the plane. A geodesic on a plane is a straight line. So, the straight line is exactly what we need. Moreover, we can see that the loop does not slip off the top of the mountain only if the angle B at the top of the sector does not exceed 180o as depicted on Fig.(b). Otherwise (see Fig.(c)), the line lies outside the sector and the loop has no equilibrium on the cone.
To find the critical angle A of the cone, we note that if L is the generatrix of the cone, then the length of the arc, which subtends the angle B, equals the circumference of the base of the cone 2{pi}r, where r is the radius of the base: B L = 2 {pi} r. As r = L sin(A) and the critical angle B = {pi}, sin(A) = 0.5, and therefore A= 30o.
P.S. An interesting related problem can be found in the book Riemannian Geometry by S.Gallot, D.Hulin and J.Lafontaine (Springer Verlag, 1987 (1st edition), 1990 (2nd edition)).
P.P.S. (5/2001) Pavel Novikov from Institute of Semiconductor Physics, Russian Academy of Science (Siberian Branch) (e-mail novikov@isp.nsc.ru) wrote us the following:
In 1982, when I studied in the Novosibirsk State University (Russia), Dr. Spector lead seminars for us on Continious Media Physics and I heard the same problem from him. He gave us only 5 minutes to solve the problem. Nobody did and he told us an answer... By the way only three my friends solved this beautiful problem. Now two of them work in Institute of Semiconductor Physics in the Novosibirsk Academgorodok.
 Back to "front page"
Back to "front page"