Footnote:
Aristotle's text appears in Prior Analytics, I-23, and it reads as follows:
For all who effect an argument per impossible infer syllogistically what is false, and prove the original conclusion hypothetically when something impossible results from the assumption of its contradictory; e.g. that the diagonal of the square is incommensurate with the side, because odd numbers are equal to evens if it is supposed to be commensurate. One infers syllogistically that odd numbers come out equal to evens, and one proves hypothetically the incommensurability of the diagonal, since a falsehood results through contradicting this.
The argument delineated here by Aristotle is usually attributed to Pythagoras and it is thus considered to have been the way in which the existence of incommensurable quantities was originally proved. [See for instance: Heath, T.L., Euclid - The Thirteen Books of the Elements, Translated and Edited by T.L. Heath, 2d. ed., 3 Vols., New York, Dover (1956), in Vol. 3, p. 2]. Following Heath, one might indeed see this argument as describing the modern proof of the irrationality of √2, in the following terms:
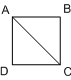
Suppose AC, the diagonal of a square, to be commensurable with AB, its side. Let a : b be their ratio expressed in the smallest numbers.
Then a > b and therefore necessarily > 1.
Now AC2 : AB2 = a2 : b2,
and since AC2 = 2AB2,
[Heath justifies this step by appeal to Proposition I.47of the Elements, i.e., the Pythagorean theorem]
a2 = 2b2.
Therefore a2 is even, and therefore a is even.
Since a : b is in its lower terms, it follows that must be odd.
Put a = 2g;
therefore 4g2 = 2b2,
or b2 = 2g2,
so that b2, and therefore b, must be even.
But is b also odd:
which is impossible.
This proof only enables us to prove the incommensurability of the diagonal of a square with its side, or of √2 with unity.
The proof is indeed based on a contradiction in which an odd number is also even, as in Aristotle's description. It is also the case that Heath takes pains to embed it into a proper geometrical context, as befits Aristotle's reference to the diagonal. Still Heath's last remark draws an equivalence between incommensurability of diagonal and side, on the one hand, and incommensurability of √2 and unity, on the other hand. Such an equivalence is itself totally foreign to the Greek conception of number, to begin with, since it assumes an abstract, general conception of what a number is. But the reader should pay special attention to the second half of the proof, where Heath uses a purely algebraic manipulation of the symbols: a, b, g.
Put a = 2g;
therefore 4g2 = 2b2,
or b2 = 2g2,
Unguru's main point in analyzing a proof like this one is that such symbolic manipulations are totally unheard of in any extant mathematical text of the period and that there is every reason to assume that they were simply unknown at the time and thus foreign to the mathematical world of the ancient Greeks. Thus, he would conclude, the proof referred to by Aristotle must have been different from this one. The kind of historiographical approach that he set out to criticize would rely on the very possibility of mathematically formulating this argument to conclude that this was indeed the argument actually used, especially since it can be accommodated with Aristotle's description. A qualm such as raised by Unguru would be simply dismissed offhand.
Is there an alternative argument that can be accommodated with Aristotle's description, that proofs the incommensurability of the diagonal and the side, and that does not invoke mathematical ideas that seem to be foreign to the relevant historical record as known to us? Unguru has suggested the following one, that relies on two pillars: (1) a diagram appearing in Plato's Meno and thus certainly known and discussed in the present context, and (2) properties of figurative numbers that were certainly known to the Pythagoreans. The diagram is the following:

And the alternative argument is the following: If DB and DH are commensurable then they represent two numbers, each of which counts how many times the said common measure respectively enters in them. It may legitimately be assumed that we can chose those numbers in such a way that they have no common factors and thus, in particular not the two of them are even. It follows from the diagram that the squares DBHI and AGFE represent two squares numbers and that, moreover, AGFE is the double of the square number DBHI. Thus, AG which is the side of AGFE (and equals DH) is an even number (a result know to the Pythagoreans from their research on figurative numbers). Thus, the square built on AG, AGFE is divisible by four, and therefore the square ABCD, which is one quarter of AGFE, represents itself a number. But DBHU is a square which is the double of ABCD, and therefore it represents a square even number, and therefore its side, DB represents itself an even number. But this contradicts the assumption that DB an DH are not both even numbers.
Fictional Narrative and the History of Mathematics
Leo Corry - Tel Aviv University